Hệ vật "lò xo - vật - Trái Đất" là hệ cô lập (do không chịu ngoại lực tác dụng) nên cơ năng của hệ vật bảo toàn.

Chọn mặt phẳng ngang đi qua vị trí A làm mốc tính thế năng trọng trường ( W t  = 0) và chọn vị trí lò xo không bị biến dạng làm mốc thế năng đàn hồi ( W đ h  = 0). Khi đó cơ năng của hệ vật tại vị trí bất kì có giá trị bằng tổng của động năng  W đ  thế năng trọng trường  W t  và thế năng đàn hồi  W đ h  :

W =  W đ  +  W t  +  W đ h  = m v 2 /2 + mgh + k ∆ l 2 /2

ại vị trí A, lò xo bị nén một đoạn ∆ l = (10 + 30). 10 - 2 = 40. 10 - 2  m, vật có động năng  W đ (A) = 0 và thế năng trọng trường  W t (A) = 0, nên cơ năng của hệ vật tại A đúng bằng thế năng đàn hồi của lò xo :

W(A) =  W đ h (A) = k ∆ l 2 /2 = 800. 40 . 10 - 2 2  = 64(J)

Khi buông nhẹ tay để thả cho vật từ vị trí A chuyển động lên phía trên tới vị trí B cách A một đoạn  ∆ l = 40 cm, tại đó lò xo không bị biến dạng, thế năng đàn hồi  W đ h  = 0. Sau đó, vật tiếp tục chuyển động từ vị trí B lên tới vị

trí C có độ cao h m a x = BC, tại đó vật có vận tốc v C  = 0 và động năng  W đ  (C) = 0, nên cơ năng của hệ vật tại C bằng :

W(C) = mg( ∆ l +  h m a x ) + k h m a x 2 /2

Áp dụng định luật bảo toàn cơ năng cho chuyển động của hệ vật từ vị trí A qua vị trí B tới vị trí C, ta có :

W(C) = W(B) = W(A) ⇒ mg( ∆ l +  h m a x ) + k h m a x 2 /2 = 64

Thay số, ta tìm được độ cao  h m a x  = BC :

8.10.(40. 10 - 2  +  h m a x ) + 800. h m a x /2 = 64 ⇒ 50 h 2  + 10h - 4 = 0

Phương trình này có nghiệm số dương :  h m a x  = BC = 20 cm.

Như vậy, độ cao lớn nhất mà vật đạt tới so với vị trí A bằng :

H m a x  = AB + BC = 40 + 20 = 60 cm

Bài này theo bảo toàn cơ năng thì độ cao lớn nhất mà vật đạt được so với vị trí cân bằng là 20 cm (bằng độ nén khi ấn xuống)

Năng lượng của hệ dự trữ dưới dạng thế năng đàn hồi

⇒ Đáp án B

Chọn đáp án B

Hệ vật "Lò xo — Vật trượt -Trái Đất" là hệ cô lập (do không chịu ngoại lực tác dụng) nên cơ năng của hệ vật bảo toàn.

Chọn mặt phẳng ngang làm mốc thế năng trọng trường ( W t  = 0) và chọn vị trí cân bằng của vật tại điểm O làm mốc thế năng đàn hồi ( W đ h  = 0). Vì hệ vật chuyển động trên cùng mặt phẳng ngang, nên cơ năng của hệ vật tại vị trí bất kì có giá trị bằng tổng của thế năng đàn hồi và động năng :

W =  W đ h  +  W đ  = k ∆ l 2 /2 + m v 2 /2

Muốn xác định công suất của lực đàn hồi, ta phải tính được lực đàn hồi của lò xo và vận tốc của vật tại cùng một vị trí.

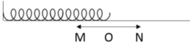
Chọn chiểu lò xo bị nén là chiều dương. Tại vị trí A : lò xo bị nén một đoạn Δl = 10 cm > 0 và vật rời xa vị trí cân bằng có vận tốc v > 0, nên lực đàn hồi của lò xo (chống lại lực nén) ngược hướng với vận tốc của vật và có giá trị bằng :

F đ h  = -k ∆ l =-500. 10. 10 - 2  = -50N < 0

Cơ năng của hệ vật tại vị trí A bằng :

W(A) = W(O) ⇒ m v A 2 /2 + k ∆ l 2 /2 = m v 0 2 /2

Hay:

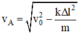
Thay số, ta tìm được vận tốc của vật trượt tại vị trí A :

Từ đó suy ra công suất của lực đàn hồi tại vị trí A có độ lớn bằng :

P = | F đ h v A | = 50.3 = 150 W

Đáp án B

Tại vị trí lò xo nén 10cm, cơ năng dàn hồi của vật bằng:

1 2 m v 2 + 1 2 k Δ l 2 = 1 2 500 0 , 1 2 = 2 , 5 J

Cơ năng đó có giá trị bằng động năng tại vị trí cân bằng

( thế năng bằng 0 ở vị trí cân bằng )

Đáp án A