Cho hàm số 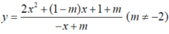 có đồ thị
(
C
m
)
và A là điểm cố định có hoành độ âm của
(
C
m
)
. Giá trị của để tiếp tuyến tại A của
(
C
m
)
vuông góc với đường phân giác góc phần tư thứ nhất là
có đồ thị
(
C
m
)
và A là điểm cố định có hoành độ âm của
(
C
m
)
. Giá trị của để tiếp tuyến tại A của
(
C
m
)
vuông góc với đường phân giác góc phần tư thứ nhất là
A.![]()
B. ![]()
C. ![]()
D. 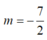

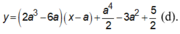
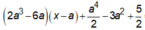
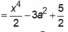
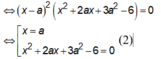
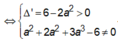
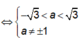


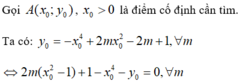
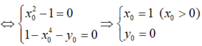

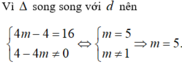
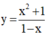
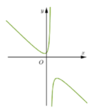
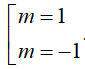
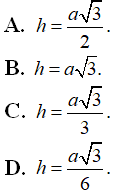
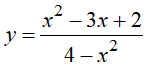 là:
là: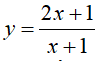 có đồ thị (C). Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ hai điểm A(2;4) và B(-4;-2) đến tiếp tuyến của (C) tại M là bằng nhau
có đồ thị (C). Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ hai điểm A(2;4) và B(-4;-2) đến tiếp tuyến của (C) tại M là bằng nhau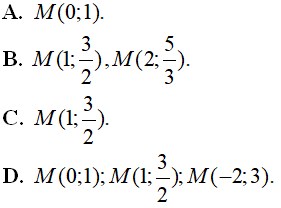 giúp mik nhe r mik tick choa pls
giúp mik nhe r mik tick choa pls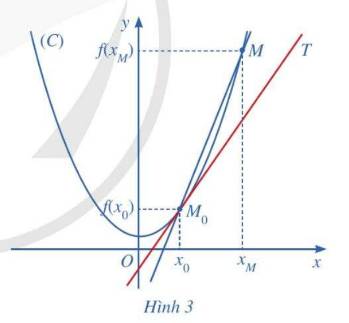
Đáp án A
Gọi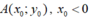 là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có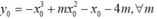
Lại có
Phương trình tiếp tuyến của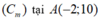 có dạng
có dạng
Đường phân giác góc phần tư thứ nhất có phương trình d: y = x.
Vì ∆ vuông góc với d nên ta có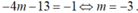 .
.