Cho hàm số y = f x có đạo hàm liên tục trên đoạn 1 ; 4 , đồng biến trên đoạn 1 ; 4 và thỏa mãn đẳng thức x + 2 x . f x = f ' x 2 , ∀ x ∈ 1 ; 4 . Biết rằng f 1 = 3 2 , tính I = ∫ 1 4 f x d x ?
A. I = 1186 45 .
B. I = 1174 45 .
C. I = 1222 45 .
D. I = 1201 45 .

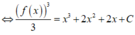
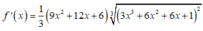
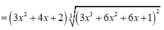
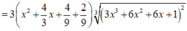
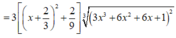
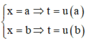
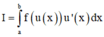






Đáp án A.
Vì y = f x là hàm số đồng biến trên 1 ; 4 ⇒ f x ≥ f 1 = 3 2 .
Khi đó:
x + 2 x . f x = f ' x 2 ⇔ x . 2 f x + 1 = f ' x ⇔ f ' x 2 f x + 1 = x ( * ) .
Lấy nguyên hàm 2 vế của (*), ta được:
∫ f ' x 2 f x + 1 d x = ∫ x d x = 2 3 x x + C ( 1 ) .
Đặt t = 2 f x + 1
⇔ d t = f ' x 2 f x + 1 d x ⇒ ∫ f ' x 2 f x + 1 d x = ∫ d t = t ( 2 ) .
Từ (1), (2) suy ra 2 f x + 1 = 2 3 x x + C mà f 1 = 2 3 ⇒ 2. 3 2 + 1 = C + 2 3 ⇔ C = 4 3 .
Do đó:
2 f x + 1 = 2 3 x x + 4 3 ⇔ f x = 1 2 2 3 x x + 4 3 2 − 1 .
Vậy ∫ 1 4 f x d x = 1186 45 .