Tìm các giá trị của tham số m để hàm số y = m x 4 + ( m - 1 ) x 2 + m chỉ có đúng một cực trị
A. 0 < m ≤ 1 .
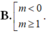
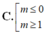
D. 0 ≤ m ≤ 1 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+) Trường hợp 1: m = 0
Ta có hàm số: y = -x2, hàm số này có 1 cực trị.
Vậy m = 0 thỏa mãn.
+) Trường hợp 2: m ≠ 0
![]()
![]()

![]()
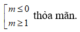

- Với \(m=0\Rightarrow y=-x^2-2\) chỉ có cực đại (thỏa mãn)
- Với \(m\ne0\) hàm chỉ có cực đại khi:
\(\left\{{}\begin{matrix}m< 0\\m\left(2m-1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
Vậy \(m\le0\)

Đáp án C
Với m = − 1 ⇒ y = − 1 hàm số không có cực trị.
Với m ≠ 1.
Hàm số có 1 cực trị ⇔ a b = m + 1 m 2 − 1 ≥ 0
⇔ m + 1 2 m − 1 ≤ 0 ⇔ m ≤ 1.
Kết hợp 2 TH suy ra m ≤ 1 , m ≠ − 1.

Đáp án A
Ta có ![]() Hàm số có đúng môt cực trị
Hàm số có đúng môt cực trị
![]() đổi dấu một lần trên R
đổi dấu một lần trên R ![]()

y' = 4(m - 1) x 3 - 2mx = 2x[2(m - 1) x 2 - m]
Hàm số có đúng một cực trị khi y' = 0 có đúng một nghiệm, tức là
2x[2(m - 1) x 2 - m] = 0 chỉ có nghiệm x = 0
Muốn vậy, phải có m = 1 hoặc 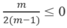
⇒ 0 ≤ m ≤ 1.
Vậy với 0 ≤ m ≤ 1 hàm số đã cho có một cực trị duy nhất.
Chọn C
Trường hợp 1: m = 0
Ta có hàm số: y = - x 2 , hàm số này có 1 cực trị.
Vậy m = 0 thỏa mãn.
Trường hợp 2: m ≠ 0
y ' = 4 m x 3 + 2 ( m - 1 ) x
Hàm số có đúng 1 cực trị.
Kết hợp TH1 và TH2