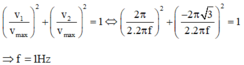\(\Delta\varphi=\omega\Delta t=2\left(rad\right)\) \(\Rightarrow\) \(\left\{{}\begin{matrix}\text{S}_{max}=2Asin\dfrac{\Delta\varphi}{\text{2}}=2.10sin1\approx\text{16,83(cm)}\\\text{S}_{\text{min}}=\text{2A}\left(\text{1-cos}\dfrac{\Delta\varphi}{\text{2}}\right)=2.10\left(\text{1-cos1}\right)\approx\text{9,19(cm)}\end{matrix}\right.\)

Tham khảo:

\(\Delta\varphi=\omega\Delta t=2\left(rad/s\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}S_{max}=2Asin\dfrac{\Delta\varphi}{2}=2\cdot10sin1\approx16,8\left(cm\right)\\S_{min}=2A\left(1-cos\dfrac{\Delta\varphi}{2}\right)=2\cdot10\cdot\left(1-cos1\right)\approx9,19\left(cm\right)\end{matrix}\right.\)

Chọn D.

Thòi gian dài nhất ứng với vật đi chậm nhất => Vật đi xung quanh vị trí biên (vd biên x = A), đi từ x = A/2 đến x = A rồi về x = A/2. Thời gian đi đó sẽ là:

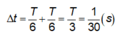
Chọn đáp án A.

Vận tốc góc ω = π rad/s

=> Tần số góc của dao động điều hòa tương ứng là ω = π (rad/s)

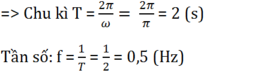
Đáp án A.

Khoảng thời gian ngắn nhất để vận tốc thay đổi từ 2 π  cm/s  đến - 2 π 3  cm/s là  T 4

 Hai thời điểm này vuông pha với nhau

:

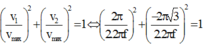
Đáp án A. 

Khoảng thời gian ngắn nhất để vận tốc thay đổi từ  2 π cm/s đến  - 2 π 3 cm/s là  T 4

⇒ Hai thời điểm này vuông pha với nhau : 

Đáp án A