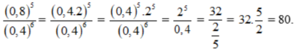
Lời giải

0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

= (1 + 9) + (2 + 8) + (3 + 7) + ( 4 + 6) + 10 + 5

= 10 + 10 + 10 + 10 + 10 + 5

= 55

Vậy đáp án đúng là B

`a, (2 \times 6) \times 4`

`= 12 \times 4=48`

`2 \times (6 \times 4)`

`= 2 \times 24 = 48`

` (8 \times 5) \times 2`

`= 40 \times 2=80`

` 8 \times (5 \times 2)`

` 8 \times 10 = 80`

`b,` Giá trị của `2` biểu thức `(2 \times 6) \times 4, 2 \times (6 \times 4)`  bằng nhau `(=48)`

`-` Giá trị của `2` biểu thức `(8 \times 5) \times 2, 8 \times (5 \times 2)` bằng nhau `(=80)`

`c,`

` 25 \times (2 \times 2) =25 \times 4 = 100`

` (25 \times 2) \times 2= 50 \times 2 = 100 `

a) Các phép chia sai: 32 : 6 = 5 (dư 1); 9 : 8 = 1 (dư 0).

Sửa lại:

32 : 6 = 5 (dư 2)

9 : 8 = 1 (dư 1)

b) Ta có thể đặt dấu ngoặc như sau:

(3 + 4) × 9 = 63

9 : (3 + 6) = 1

(16 – 16) : 2 = 0

12 : (3 × 2) = 2

\(\begin{array}{l}a)\frac{{{3^{12}} + {3^{15}}}}{{1 + {3^3}}}\\ = \frac{{{3^{12}} + {3^{12}}{{.3}^3}}}{{1 + {3^3}}}\\ = \frac{{{3^{12}}.(1 + {3^3})}}{{1 + {3^3}}}\\ = {3^{12}}\\b)2:{\left( {\frac{1}{2} - \frac{2}{3}} \right)^2} + 0,{125^3}{.8^3} - {( - 12)^4}:{6^4}\\ = 2:{\left( {\frac{3}{6} - \frac{4}{6}} \right)^2} + {(0,125.8)^3} - {12^4}:{6^4}\\ = 2:{\left( {\frac{{ - 1}}{6}} \right)^2} + {1^3} - {(\frac{{12}}{6})^4}\\ = 2:\frac{1}{{36}} + 1 - {2^4}\\ = 2.36 + 1 - 16\\ = 72 + 1 - 16=57\end{array}\)

\(a,ĐK:x\ne\pm2\\ A=\dfrac{4x-8+2x+4-5x+6}{\left(x-2\right)\left(x+2\right)}=\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x-2}\\ ĐK:x\ne-1;x\ne-2\\ B=\dfrac{x+1}{\left(x+1\right)\left(x+2\right)}=\dfrac{1}{x+2}\\ b,x^2+x=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\\ \forall x=0\Leftrightarrow A=\dfrac{1}{0-2}=-\dfrac{1}{2}\\ \forall x=-1\Leftrightarrow A=\dfrac{1}{-1-2}=-\dfrac{1}{3}\)

\(x^2+2x=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-2\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=0\\ \Leftrightarrow B=\dfrac{1}{0+2}=\dfrac{1}{2}\)

Mỗi biểu thức thường có nhiều cách viết. Dưới đây là một trong các cách viết:

       ( 5 – 5 ) x 5 x 5 x 5 = 0 ( bất cứ số nào nhân với 0 cũng bằng 0 )

                        ( 5 + 5 ) : 5 – 5 : 5          = 1

      ( 5 + 5 ) : 5 + ( 5 – 5 )    = 2

                        ( 5 + 5 ) : 5 + 5 : 5         = 3

                        ( 5 + 5 + 5 + 5 ) : 5        = 4

                        5 : 5 x 5 : 5 x 5              = 5

                        5  : 5 + 5 : 5 x 5            = 6

                        5 : 5 + 5 : 5 + 5             = 7

                        ( 5 + 5 + 5 ) : 5 + 5       = 8

                        ( 55 – 5 – 5 ) : 5             = 9

                       5 x 5 – ( 5 + 5 + 5 )       = 10

a, ( 3 - 0,6) - ( 7 + 3\(\dfrac{1}{4}\) - \(\dfrac{8}{5}\)) - ( 9 - 2\(\dfrac{1}{4}\))

 = 2,4 - (7 + 3,25 - 1,6) - (9 - 2,25)

= 2,4 - 7 - 3,25 + 1,6 - 9 + 2,25

= (2,4 + 1,6) - (7+ 9) - ( 3,25 - 2,25)

= 4 - 16 - 1

= - 12 - 1

= -13

b, ( - \(\dfrac{5}{8}\) + \(\dfrac{7}{6}\) - \(\dfrac{0}{8}\)) - (\(\dfrac{5}{6}\) - \(\dfrac{7}{8}\) - 1,4) + ( \(\dfrac{3}{4}\) + \(\dfrac{5}{3}\) + \(\dfrac{12}{5}\))

 = - \(\dfrac{5}{8}\) + \(\dfrac{7}{6}\) - \(\dfrac{5}{6}\) + \(\dfrac{7}{8}\) + \(\dfrac{7}{5}\) + \(\dfrac{3}{4}\) +  \(\dfrac{5}{3}\) + \(\dfrac{12}{5}\)

= (- \(\dfrac{5}{8}\) + \(\dfrac{7}{8}\)) + (\(\dfrac{7}{6}\) - \(\dfrac{5}{6}\)) + ( \(\dfrac{7}{5}\) + \(\dfrac{12}{5}\)) + \(\dfrac{3}{4}\) + \(\dfrac{5}{3}\)

= \(\dfrac{1}{4}\) + \(\dfrac{1}{3}\) + \(\dfrac{19}{5}\) + \(\dfrac{3}{4}\) + \(\dfrac{5}{3}\)

= (\(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)) + ( \(\dfrac{1}{3}\) + \(\dfrac{5}{3}\)) + \(\dfrac{19}{5}\)

= 1 + 2 + 3,8

= 6,8

\(\frac{4^6.9^5+6^9.120}{8^4.3^{12}-6^{11}}\)

\(=\frac{\left(2^2\right)^6.\left(3^2\right)^5+\left(2.3\right)^9.2^3.3.5}{\left(2^3\right)^4.3^{12}-\left(2.3\right)^{11}}\)

\(=\frac{2^{12}.3^{10}+2^9.3^9.2^3.3.5}{2^{12}.3^{12}-2^{11}.3^{11}}\)

\(=\frac{2^{12}.3^{10}.\left(1+5\right)}{2^{11}.3^{11}.\left(2.3-1\right)}\)

\(=\frac{2.6}{3.5}\)

\(=\frac{4}{5}\)

Ta có: \(\frac{4^6\cdot9^5+6^9\cdot120}{8^4\cdot3^{12}-6^{11}}\)

\(=\frac{2^{12}\cdot3^{10}+2^3\cdot3\cdot5\cdot2^9\cdot3^9}{2^{12}\cdot3^{12}-2^{11}\cdot3^{11}}\)

\(=\frac{2^{12}\cdot3^{10}+2^{12}\cdot3^{10}\cdot5}{2^{12}\cdot3^{12}-2^{11}\cdot3^{11}}\)

\(=\frac{2^{12}\cdot3^{10}\cdot\left(1+5\right)}{2^{11}\cdot3^{11}\left(2\cdot3-1\right)}\)

\(=\frac{2\cdot6}{3\cdot5}=\frac{4}{5}\)