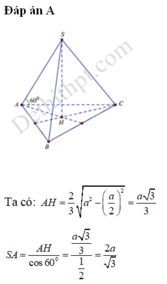
Đáp án A

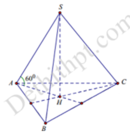
Ta có: A H = 2 3 a 2 − a 2 2 = a 3 3  

S A = A H cos 60 0 = a 3 3 1 2 = 2 a 3  

Gọi O là tâm đáy, M là trung điểm AB 

Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABC\right)\\OM\perp AB\end{matrix}\right.\) \(\Rightarrow\widehat{SMO}\) hay là góc giữa mặt bên và mặt đáy

\(\Rightarrow\widehat{SMO}=60^0\) \(\Rightarrow SO=OM.tan60^0=\dfrac{1}{3}CM.tan60^0=\dfrac{1}{3}AB.\dfrac{\sqrt{3}}{2}.tan60^0=\dfrac{a}{2}\)

\(CO=\dfrac{2}{3}CM=\dfrac{2}{3}.AB\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)

\(SC=\sqrt{SO^2+OC^2}=\dfrac{a\sqrt{21}}{6}\)

Đáp án A

Gọi H là hình chiếu của S lên lên (ABCD).

A H = 2 3 a 2 - a 2 2 = a 3 3 S H = A H tan 60 ∘ = a 3 3 . 3 = a

Thể tích khối chóp là: 

V = 1 3 S A B C · S H = 1 3 · 1 2 a 2 sin 60 ° . a = a 3 . 3 12

Lời giải:

$H$ là chân đường cao của hình chóp đều nên $H$ chính là tâm đường tròn ngoại tiếp tam giác $ABC$

Kẻ $HM\perp BC$. Dễ thấy $M$ là trung điểm $BC$ và $SBC$ cân tại $S$ nên $SM\perp BC$

Do đó:

$\angle ((SBC), (ABC))=\angle (SM, HM)$

$=\widehat{SMH}=60^0$

$\frac{SH}{HM}=\tan \widehat{SMH}=\tan 60^0=\sqrt{3}$

$\Rightarrow SH=\sqrt{3}HM$

Mà: $HM=\frac{1}{3}AM=\frac{1}{3}.\sqrt{AB^2-BM^2}=\frac{1}{3}\sqrt{AB^2-(\frac{BC}{2})^2}=\frac{\sqrt{3}}{6}a$

Do đó: $SH=\sqrt{3}HM=\frac{3}{6}a=\frac{1}{2}a$

Thầy/cô vẽ hình giúp em với ạ 

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\)

\(\Rightarrow\widehat{SAO}=60^0\Rightarrow AO=SA.cos60^0=a\)

\(R=a;l=2a\Rightarrow h=SO=\sqrt{\left(2a\right)^2-a^2}=a\sqrt{3}\)

\(V=\dfrac{1}{3}\pi R^2h=\dfrac{\sqrt{3}}{3}\pi a^3\)

Chọn đáp án A