Cho hình lập phương ABCDA'B'C'D'có cạnh bằng a. Gọi M là điểm thuộc cạnh AB sao cho AM= 1 3 A B . Tính khoảng cách h từ điểm C tới mặt phẳng (B'DM).

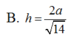
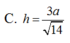
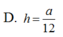
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
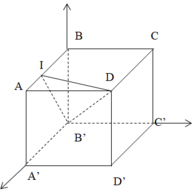
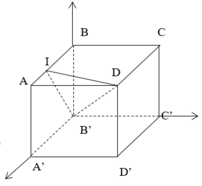
Chọn hệ trục tọa độ như hình vẽ
B ' ( 0 ; 0 ; 0 ) , D ( a ; a ; a ) , I ( 2 a 3 ; 0 ; a ) , C ( 0 ; a ; a ) B ' D → ( a ; a ; a ) , B ' I → ( 2 a 3 ; 0 ; a ) ⇒ n → = [ B ' D → , B ' I → ] = ( a 2 ; − a 2 3 ; − 2 3 a 2 ) ⇒ ( B ' I D ) : 3 x − y − 2 z = 0 ⇒ d ( C , ( B ' I D ) ) = 3 a 14

Đáp án D
Chọn hệ trục tọa độ như hình vẽ
B ' 0 ; 0 ; 0 , D a ; a ; a , I 2 a 3 ; 0 ; a , C 0 ; a ; a B ' D → a ; a ; a , B ' I → 2 a 3 ; 0 ; a ⇒ n → = B ' D → ; B ' I → = a 2 ; - a 2 3 ; - 2 3 a 2 ⇒ B ' I D : 3 x - y - 2 z = 0 ⇒ d C ; B ' I D = 3 a 14

\(BP=\dfrac{1}{3}AB\Rightarrow BP=\dfrac{1}{2}AP\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}d\left(A;\left(SPC\right)\right)\)
Trong tam giác APC, kẻ \(AH\perp CP\Rightarrow CP\left(SAH\right)\)
Trong tam giác vuông SAH, kẻ \(AK\perp SH\Rightarrow AK\perp\left(SPC\right)\Rightarrow AK=d\left(A;\left(SPC\right)\right)\)
\(AP=\dfrac{2}{3}AB=\dfrac{2a}{3}\Rightarrow CP=\sqrt{AP^2+AC^2-2AP.AC.cos60^0}=\dfrac{a\sqrt{7}}{3}\)
Áp dụng định lý hàm sin:
\(\dfrac{AP}{sin\widehat{ACP}}=\dfrac{CP}{sinA}\Rightarrow sin\widehat{ACP}=\dfrac{AP.sin60^0}{CP}=\dfrac{\sqrt{21}}{7}\)
\(\Rightarrow AH=AC.sin\widehat{ACP}=\dfrac{a\sqrt{21}}{7}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}\Rightarrow AK=\dfrac{SA.AH}{\sqrt{SA^2+AH^2}}=\dfrac{2a\sqrt{93}}{31}\)
\(\Rightarrow d\left(B;\left(SPC\right)\right)=\dfrac{1}{2}AK=\dfrac{a\sqrt{93}}{31}\)
Bạn kiểm tra lại phần tính toán
Đáp án C