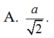
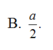
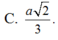
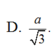
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Ý tưởng: 1 - MN phải chăng sẽ là hai điểm đặc biệt nào đó
2 – Khi nhận ra M là trung điểm của BA’ thì ta tiến hành tính toán MN qua điểm A’ bằng cách lấy P thuộc BC’!
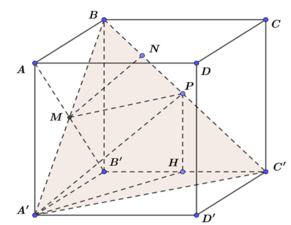
Dễ có mặt phẳng (BA’C’) vuông góc với AB’. Do đó để MN là nhỏ nhất thì M là giao của AB’ và BA’, N là điểm thuộc BC’ sao cho góc giữa MN và (A’B’C’D’) là 30 ° . Gọi P là điểm thuộc BC’sao cho A’P cũng hợp với mặt phẳng đáy một góc 30 ° , khi đó MN là đường trung bình của tam giác BA’P nên M N = 1 2 A ' P .
Giả sử độ dài đoạn B’H = x, khi đó PH = HC’ = a – x (tam giác PC’H vuông cân tại C’), và A ' H = A ' B ' 2 + B ' H 2 = a 2 + x 2 . Theo điều ta đã giả sử ở trên thì góc giữa A’P và (A’B’C’D’) = 30 ° , do đó
tan P A ' H ^ = P H A ' H = a − x a 2 + x 2 = 3 3 hay a 2 + x 2 = 3 a − x (1)
Mặt khác ta lại có
A ' P = A ' H 2 + H P 2 = a 2 + x 2 + ( a − x ) 2 = 4 a − x 2 = 2 a − x (2)
Từ (1) và (2) ta tính được A ' P = 4 a 5 + 1 . Từ đây ta rút ra được M N = 2 a 5 + 1 .
Chọn phương án D.
Gọi G là trung điểm của CD. Cho MN cắt AG tại I. Ta sẽ chứng minh điểm I cố định.
Thật vậy: Kéo dài tia BG cắt tia AD tại P. Qua 2 điểm B và P kẻ các đường thẳng song song với MN, chúng cắt đường thẳng AG lần lượt ở 2 điểm E và F.
Dễ thấy: \(\Delta\)BGC = \(\Delta\)PGD (g.c.g) => GB = GP (2 cạnh tương ứng)
=> \(\Delta\)BEG = \(\Delta\)PFG (g.c.g) => GE = GF (2 cạnh tương ứng) => EF = 2.GE
Xét \(\Delta\)PAF có: N thuộc AP; I thuộc AF; IN // PF => \(\frac{AP}{AN}=\frac{AF}{AI}=\frac{AE+EF}{AI}=\frac{AE+2.GE}{AI}\)(ĐL Thales)
Do \(\Delta\)BGC = \(\Delta\)PGD (cmt) nên BC = PD. Mà BC = AD => PD = AD = 1/2 .AP
\(\Rightarrow\frac{2.AD}{AN}=\frac{AE+2.GE}{AI}\). Tương tự: \(\frac{AB}{AM}=\frac{AE}{AI}\)
Do đó: \(\frac{AB}{AM}+\frac{2.AD}{AN}=\frac{2\left(AE+GE\right)}{AI}=\frac{2.AG}{AI}\). Suy ra \(\frac{2.AG}{AI}=4\)(Theo gt)
\(\Rightarrow\frac{AG}{AI}=2\)=> I là trung điểm của AG
Ta thấy: Hbh ABCD cố định có G là trung điểm CD nên AG cố định. Mà I là trung điểm AG nên I cũng cố định.
Lại có: MN đi qua I nên MN luôn đi qua 1 điểm cố định (đpcm).
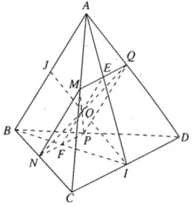
a)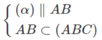 
⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và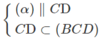 
Nên ⇒ (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD)
Và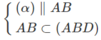 
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
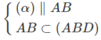nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có
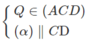
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ .
Vậy tập hợp các điểm O là đoạn IJ.
Đáp án A