Một công ty Container cần thiết kết các thùng đựng hàng hình hộp chữ nhật, không nắp, có đáy hình vuông, thể tích là 108 m 3 . Tìm tổng diện tích nhỏ nhất của các mặt xung quanh và mặt đáy
![]()
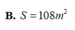
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x,y > 0 lần lượt là chiều dài cạnh đáy và chiều cao của hình hộp
Tổng diện tích xung quanh và diện tích của một mặt đáy của thùng đựng hành là S = x 2 + 4 x y
Thể tích của thùng đựng hàng là
V = x 2 y = 108 ⇒ y = 108 x 2
Suy ra S = x 2 + 4 x . 108 x 2 = x 2 + 432 x
Tìm giá trị nhỏ nhất của S trên khoảng 0 ; + ∞
Ta có
S ' = 2 x - 432 x 2 ; S ' = 0 ⇔ x = 6 S ' ' = 2 + 864 x 3 > 0 , ∀ x ∈ 0 ; + ∞
Suy ra S = S(6) = 108. Vậy diện tích nhỏ nhất cần tìm là 108 m 2
Đáp án B

Đáp án là A
Gọi cạnh đáy, cạnh bên của hình hộp đứng lần lượt là x và y ( x ,y > 0)
Ta có:
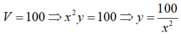
Khi đó:
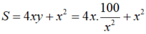
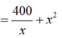
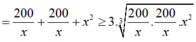
![]()
Vậy S đạt giá trị nhỏ nhất bằng 30 40 3 khi
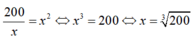

Đáp án C
Phương pháp: Lập hàm số chi phí theo một ẩn sau đó tìm giá trị nhỏ nhất của hàm số đó.
Cách giải: Gọi a là chiều dài cạnh đáy hình vuông của hình hộp chữ nhật và b là chiều cao của hình hộp chữ nhật ta có a 2 b = 8 a , b > 0 ⇒ a b = 8 a
Diện tích đáy hình hộp là a 2 và diện tích xung quanh là 4ab nên chi phí để làm thùng tôn là 100 a 2 + 50.4 a b = 100 a 2 + 200 a b = 100 a 2 = 100. 8 a = 100 a 2 + 1600 a = 100 a 2 + 16 a
Áp dụng BĐT Cauchy ta có a 2 + 16 a = a 2 + 8 a + 8 a ≥ 3 a 2 + 8 a + 8 a 3 = 3.4 = 12
Dấu bằng xảy ra khi và chỉ khi a 2 + 8 a ⇔ a = 2.
Vậy chi phí nhỏ nhất bằng 1200000 đồng khi và chỉ khi cạnh đáy hình hộp bằng 2m.

a, Thể tích thùng: 3 x 2 x 1,5 = 9 (m3)
Diện tích xung quanh thùng: 2 x 1,5 x (3 + 2) = 15 (m2)
b, Số tiền phải trả khi sơn xung quanh thùng:
15 x 120 000 = 1 800 000 (đồng)
Đ.số:......

Đáp án B
Ta có
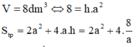
Ta tìm điều kiện của a đê diện tích toàn phần nhỏ nhất. xét hàm số ta được a=2
Đáp án B