Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}\ne-\dfrac{1}{m}\)

=>\(m^2\ne-3\)(luôn đúng)

\(\left\{{}\begin{matrix}mx-y=2\\3x+my=5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\cdot\left(mx-2\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5+2m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-2\\x=\dfrac{2m+5}{m^2+3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m+5}{m^2+3}\\y=\dfrac{2m^2+5m}{m^2+3}-2=\dfrac{2m^2+5m-2m^2-6}{m^2+3}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{2m+5}{m^2+3}\\y=\dfrac{5m-6}{m^2+3}\end{matrix}\right.\)

\(x+y=\dfrac{3}{m^2+3}\)

=>\(\dfrac{2m+5+5m-6}{m^2+3}=\dfrac{3}{m^2+3}\)

=>\(7m-1=3\)

=>7m=4

=>m=4/7(nhận)

1) điều kiện của m: m khác 5/2

thế x=2 vào pt1 ta đc:

(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)

lập △'=[-(m-1)]²-*(2m-5)*3 = (m-4)²

vì (m-4)² ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2

3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m

Xét hệ x − ( m − 2 ) y = 2 ( m − 1 ) x − 2 y = m − 5

⇔ ( m − 2 ) y = x − 2 2 y = ( m − 1 ) x − m + 5 ⇔ ( m − 2 ) y = x − 2 y = m − 1 2 x − m 2 + 5 2

TH1: Với m – 2 = 0 ⇔ m = 2 ta có hệ 0. y = x − 2 y = 1 2 x + 3 2 ⇔ x = 2 y = 1 2 x + 3 2

Nhận thấy hệ này có nghiệm duy nhất vì hai đường thẳng x = 2 và y = 1 2 x + 3 2 cắt nhau

TH2: Với m – 2 ≠ 0 ⇔ m ≠ 2 ta có hệ: ( m − 2 ) y = x − 2 y = m − 1 2 x − m 2 + 5 2 ⇔ y = 1 m − 2 x − 2 m − 2 y = m − 1 2 x − m 2 + 5 2

Để hệ phương trình đã cho có nghiệm duy nhất thì hai đường thẳng: d : y = 1 m − 2 x − 2 m − 2 và d ' : y = m − 1 2 x − m 2 + 5 2 cắt nhau

⇔ 1 m − 2 ≠ m − 1 2 ⇔ m   –   1 m   –   2 ≠ 2 ⇔   m 2 – 3 m + 2 ≠ 2   ⇔ m 2 – 3 m   0

Suy ra m ≠ {0; 2; 3}

Kết hợp cả TH1 và TH2 ta có m ≠ {0; 3}

Vậy hệ phương trình đã cho có nghiệm duy nhất khi m ≠ {0; 3}

Đáp án: C

D 

(2m -4)x = 3 ↔x = \(\dfrac{3}{2m-4}\)

Để phương trình có nghiệm thì 2m - 4 ≠ 0 ↔ m ≠ 2

Đáp án: B.

Với m = 0, phương trình 2 x 3  - 5 = 0 có nghiệm duy nhất.

Với m ≠ 0, đồ thị hàm số y = 2 x 3  + 3m x 2  - 5 chỉ cắt Ox tại một điểm khi y C Đ . y C T  > 0. Ta có y' = 6 x 2  + 6mx = 6x(x + m) = 0 có hai nghiệm là x = 0, x = -m; y(0) = -5, y(-m) = -2 m 3  + 3 m 3  - 5 =  m 3  - 5.

Suy ra y(0).y(-m) = -5( m 3  - 5) > 0 ⇔ m <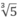 

Tìm điều kiện của tham số m để phương trình -x^2 +4x^2+m-1=0 có 4 nghiệm duy nhất

A,m>1

B,1<m<5

$\textbf{C,m<5}$

D,m>5

\(mx-x-m+2=0\)

\(x\left(m-1\right)=m-2\)

Nếu m=1 ⇒ \(0x=-1\) (vô nghiệm)

Nếu m≠1 ⇒ \(x=\dfrac{m-2}{m-1}\)

Vậy ...

Để hệ phương trình m x − 2 y = 1 2 x − m y = 2 m 2 có nghiệm duy nhất thì m 2 ≠ − 2 − m ⇔ m 2 ≠ 4 ⇔ m ≠ ± 2

Đáp án: D

Ta có pt: \(mx^2-3\left(m+1\right)x+m^2-13m-4=0\)

Do pt có nghiệm là x = -2 nên thay vào pt ta có: 

\(m\cdot\left(-2\right)^2-3\left(m+1\right)\cdot-2+m^2-13m-4=0\)

\(\Leftrightarrow4m+6\left(m+1\right)+m^2-13m-4=0\)

\(\Leftrightarrow6m+6+m^2-9m-4=0\)

\(\Leftrightarrow m^2-3m+2=0\)

\(\Delta=\left(-3\right)^2-4\cdot1\cdot2=1>0\)

\(\Leftrightarrow\left[{}\begin{matrix}m_1=\dfrac{3+\sqrt{1}}{2}=2\\m_2=\dfrac{3-\sqrt{1}}{2}=1\end{matrix}\right.\)

Nếu m = 1 thì pt là: 

\(x^2-3\left(1+1\right)x+1^2-13\cdot1-4=0\)

\(\Leftrightarrow x^2-6x-16=0\)

Theo vi-et: \(x_1+x_2=-\dfrac{-6}{1}\Rightarrow x_2=6-x_2=8\) 

Nếu m = 2 thì pt là:

\(2x^2-3\cdot\left(2+1\right)x+2^2-13\cdot2-4=0\)

\(\Leftrightarrow2x^2-9x-26=0\)  

Theo vi-et: \(x_1+x_2=-\dfrac{-9}{2}\Leftrightarrow x_2=\dfrac{9}{2}+2=\dfrac{13}{2}\)

còn một nghiệm nữa của x :v