Tìm tất cả các điểm trong mặt phẳng biểu diễn số phức z thỏa mãn điều kiện 2 z là một số thực âm
A. Trục hoành (trừ gốc tọa độ O).
B. Đường thẳng y = x (trừ gốc tọa độ O).
C. Trục tung (trừ gốc tọa độ O)
D. Đường thẳng y = -x (trừ gốc tọa độ O).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có (3-4i)z -
4
z
= 8 ![]()
Lấy môđun hai vế của (*) và sử dụng công thức ![]() ta được
ta được
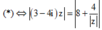
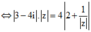
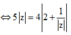
![]()
![]()
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó OM = 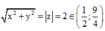

Đáp án D
Ta có 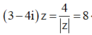
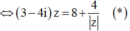
Lấy môđun hai vế của (*) và sử dụng công thức ![]() ta được
ta được
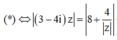

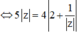
![]()
![]()
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó
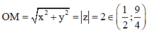

Đáp án D
Ta có 3 - 4 i z - 4 z = 8 ⇔ 3 - 4 i z = 8 + 4 z ( * )
Lấy môđun hai vế của (*) và sử dụng công thức z 1 z 2 = z 1 . z 2 , ta được
* ⇔ 3 - 4 i z = 8 + 4 z ⇔ 3 - 4 i . z = 4 2 + 1 z ⇔ 5 z = 4 2 + 1 z
⇔ 5 z 2 = 4 2 z + 1 ⇔ 5 z 2 - 8 z - 4 = 0 ⇔ z = 2
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó O M = x 2 + y 2 = z = 2 ∈ 1 2 ; 9 4 .
Đáp án C
Giả sử z = x + y i , x , y ∈ ℝ .
Ta có z 2 = x + y i 2 = x 2 - y 2 + 2 x y i
Để z 2 là một số thực âm thì x 2 - y 2 < 0 2 x y = 0 ⇔ x = 0 y ≠ 0 ⇒ biểu diễn là trục tung (trừ gốc tọa độ O)