Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + 4 = 0 . Gọi M, N là các điểm biểu diễn của các số phức z 1 , z 2 trên mặt phẳng tọa độ. Tính T = OM + ON với O là gốc tọa độ
A. T = 2 2
B. T = 8
C. T = 2
D. T = 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giải pt ta có
\(\begin{cases}z=2+\sqrt{5i}\\z=2-\sqrt{5}i\end{cases}\)
===> 2 điểm M,N lần lượt là M( 2, \(\sqrt{5}\)) VÀ N(2,-\(\sqrt{5}\))
MN=\(\sqrt{\left(2-2\right)^2+\left(-\sqrt{5}-\sqrt{5}\right)^2}\)=2\(\sqrt{5}\)

Xét phương trình \(z^2+2z+3=0\)
\(\Delta'=1-3=-2=\left(i\sqrt{2}\right)^2\)
Phương trình có 2 nghiệm \(z_1=-1+i\sqrt{2};z_2=-1-i\sqrt{2}\)
\(\Rightarrow A\left(-1;\sqrt{2}\right);B\left(-1;-\sqrt{2}\right)\)
\(AB=2\sqrt{2}\)
tìm độ dài AB là tìm modum của số phức z đúng k?
giải phương trình có 2 nghiệm phức là: z1 =-1+căn 2iz2= -1-căn 2i
và sau đó có độ dài AB là căn 3 nhá
tại mk không có phần mền dành cho tón nên các bạn thông cảm nhá.....

Đáp án A
Phương pháp.
Giả sử ![]() Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa ![]() về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm 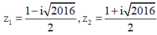
Giả sử ![]() . Từ
. Từ ![]() ta suy ra
ta suy ra
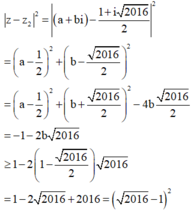
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của ![]() là
2016
-
1
là
2016
-
1
Đạt được khi và chỉ khi ![]()

Đáp án A
Phương trình z 2 − z + 2017 2 = 0 ⇔ 4 z 2 − 4 z + 2017 = 0
⇔ 2 z − 1 2 = 2016 i 2 ⇔ z 1 = 1 − i 2016 2 z 2 = 1 + i 2016 2
Ta có z − z 1 + z − z 2 ≥ z − z 1 − z − z 2 = z − z 2 ≥ z 1 − z 2 − z − z 1 = 2016 − 1
Vật giá trị nhỏ nhất của biểu thức P là P min = 2016 − 1