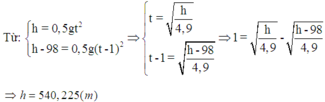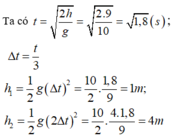Nếu có một giọt nước mưa rơi được 98 m trong giấy cuối cùng trước khi chạm đất, thì giọt nước mưa đó phải bắt đầu rơi tự do từ độ cao bao nhiêu m? Cho rằng chuyển động của giọt nước mưa là rơi tự do với g = 9,8 m/ s 2 và trong suốt quá trình rơi, khối lượng của nó không bị thay đổi.
A. 561 m.
B. 520 m.
C. 540 m.
D. 730 m.