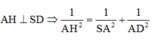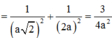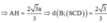Cho hình chóp S.ABCD có đáy là hình thang ABCD vuông tại A và D có AB = 2AD = 2CD, SA vuông góc với đáy (ABCD). Góc giữa SC và đáy bằng 60 ∘ . Biết khoảng cách từ B đến (SCD) là a 42 7 , khi đó tỉ số V S . A B C D a 3 bằng
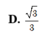
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
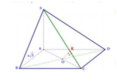
Gọi O = AC ∩ BD Kẻ OK ⊥ SC Do BD ⊥ (SAC) =>BD ⊥ OK
Do đó d(BC;SC) =OK= a 3 2
∆ S A C đ ồ n g d ạ n g ∆ O K C ( g - g )
⇒ S A O K = S C O C ⇔ x a 3 2 = x 2 + 12 a 2 a 3
⇒ x 2 = 6 a 2 ⇒ x = a 6 ⇔ S A = a 6
Khi đó: Kẻ AH ⊥ SD => AH ⊥ (SDC) => AH =d(A;(SCD))
Lại có AB//CD => AB //(SCD) => d(B;(SCD))= d(A;(SCD)=AH
∆ S A D vuông tại A có 1 A H 2 = 1 A S 2 + 1 A D 2 ⇒ A H = a 2

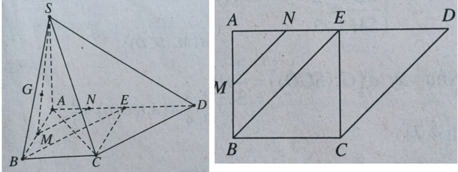
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).

Đáp án A
Phương pháp: Cách xác định góc giữa đường thẳng và mặt phẳng:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải: ABCD là hình chữ nhật ![]()
![]()
Vì SA ⊥ (ABCD) nên (SC;(ABCD)) = (SC;AC) = S C A ^
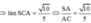
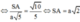
Ta có: AB//CD, CD ⊂ (SCD) => d(B;(SCD)) = d(A;(SCD))
Kẻ AH ⊥ SD, H ∈ SD
Ta có: 
![]()
Mà AH ⊥ SD => AH ⊥ (SCD) => d(A;(SCD)) = AH
Tam giác SAD vuông tại A,