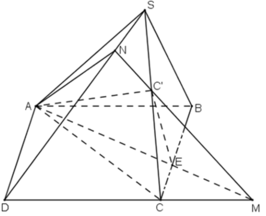
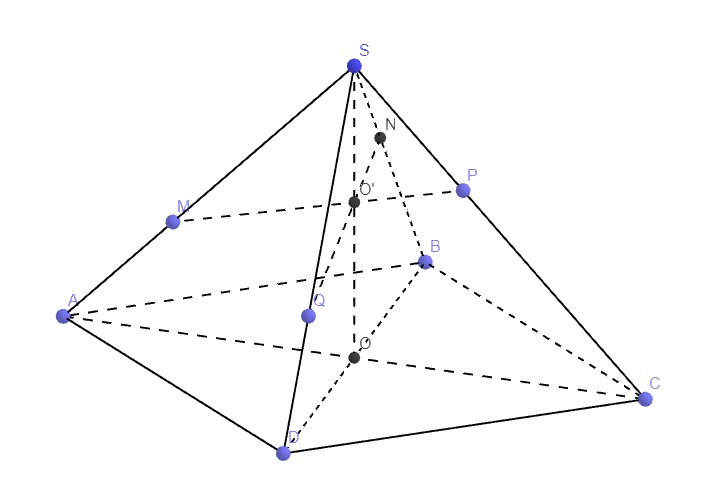
Cho hình chóp S . A B C D có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5 S M = 2 S C , mặt phẳng α qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D
A. 1 5
B. 8 35
C. 1 7
D. 6 35

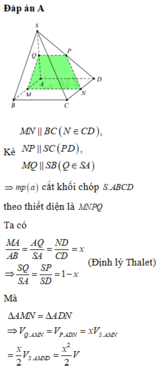
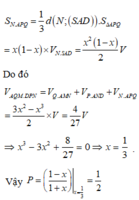
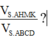
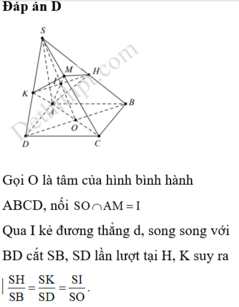



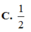
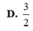
Đáp án D
Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I
Qua I kẻ đương thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra S H S B = S K S D = S I S O .
Điểm M ∈ S C thỏa mãn 5 S M = 2 S C ⇒ S M S C = 2 5
Xét tam giác SAC, có:
M S M C . A C A O . I O I S = 1 ⇒ I O S I = 4 3 ⇒ S I S O = 3 7
Khi đó:
V S . A K M V S . A D C = S K S D . S M S C ; V S . A H M V S . A B C = S H S B . S M S C
Suy ra:
V S . A H M K V S . A B C D = S M S C . S H S B = 2 5 . 3 7 = 6 35 ⇒ V S . A H M K = 6 36 V S . A B C D