Trong không gian Oxyz, cho mặt cầu S 1 có tâm I (2;1;1) bán kính bằng 4 và mặt cầu S 2 có tâm J (2;1;5) bán kính bằng 2. (P) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu S 1 , S 2 . Đặt M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ O đến mặt phẳng Giá trị M+m bằng
A. 8
B. 8 3
C. 9
D. 15

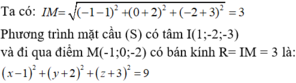
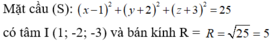



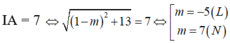

Đáp án C
Do IJ =4 > R 1 + R 2 nên hai mặt cầu cắt nhau
Giả sử IJ cắt (P) tại M ta có M J M I = R 2 R 1 = 2 => J là trung điểm của MI
=> M(2;1;9) => (P): a(x-2)+b(y-1)+c(z-9)=0 a 2 + b 2 + c 2 > 0
d(I,(P))=4 ⇔ 8 c a 2 + b 2 + c 2 = 4 ⇔ 2 c a 2 + b 2 + c 2 = 1
Do đó c ≠ 0 , chọn c=1 => a 2 + b 2 = 3
Đặt a = 3 sin t , b = 3 cos t ⇒ d ( O ; ( P ) ) = 2 a + b + 9 a 2 + b 2 + c 2 = 2 a + b + 9 2 = 2 3 sin t + 3 c o s t + 9 2
Mặt khác
- 15 ≤ 2 3 sin t + 3 cos t ≤ 15 ⇒ 9 - 15 2 ≤ d 0 ≤ 9 + 15 2 ⇒ M + m = 9