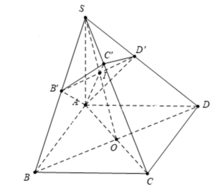
Cho hình chóp S . A B C D có đáy ABCD là hình thang, A D / / B C , A D = 3 B C . M , N lần lượt là trung điểm AB, CD. G là trọng tâm Δ S A D . Mặt phẳng G M N cắt hình chóp S . A B C D theo thiết diện là:
A. Hình bình hành
B. Δ G M N
C. Δ S M N
D. Ngũ giác






Đáp án A
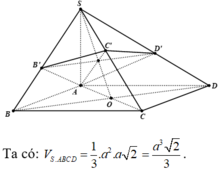
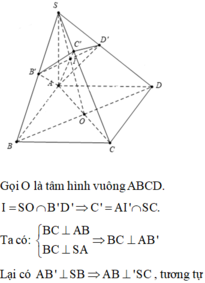
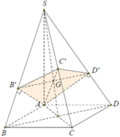
Do M N / / A D nên giao tuyến của S A D và G M N song song với AD. Khi đó qua G dựng đường thẳng song song với AD cắt SA và SD lần lượt tại Q và P. Thiết diện là hình thang MNPQ
Lại có P Q = 2 3 A D = 2 B C
Mặt khác M N = B C + A D 2 = B C + 3 B C 2 = 2 B C
Suy ra P Q = M N do thiết diện là hình bình hành