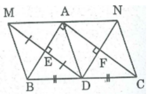
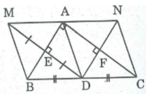
Cho tam giác ABC, biết E là trung điểm BC: AE=EB .
4.1) CM tam giác ABC là tam giác vuông
4.2) Gọi M và N lầ lượt là các điểm đối xứng với E qua AB và AC, H là giao điểm của AB và ME, K là giao điểm của AC và NE
a) Tứ giác AHEK và AMBE là hình gì? Vì sao?
b) CM 3 điểm M,A,N thẳng hàng, từ đó chứng minh M đối xứng với N qua A


đề sai r bạn ơi