Dùng định lý Vi – ét, hãy chứng tỏ rằng nếu tam thức a x 2 + bx + c có hai nghiệm x 1 , x 2 thì nó phân tích được thành a x 2 + bx + c = a(x - x 1 )(x - x 2 )
Phân tích các tam thức sau thành tích:
x 2 - 11x + 30
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ax2+bx+c=a(x2+\(\dfrac{b}{a}\)x+\(\dfrac{c}{a}\))
=a(x2-(x1+x2)x+x1x2)
=a(x-x1)(x-x2)
Áp dụng:
Câu a: Ptr có 2 nghiệm là 5,6=>x2-11x+30=(x-5)(x-6)
Câu b: Ptr có 2 nghiệm là \(\dfrac{-2}{3}\),-4=>3x2+14x+8=3(x+\(\dfrac{2}{3}\))(x+4)
Câu c: Ptr có 2 nghiệm là \(\dfrac{2}{5}\),-2=>5x2+8x-4=5(x-\(\dfrac{2}{5}\))(x+2)
Câu d: Ptr có 2 nghiệm là 3+\(\sqrt{3}\),-2+\(\sqrt{3}\)=>
x2-(1+2\(\sqrt{3}\))x-3+\(\sqrt{3}\)=(x-3-\(\sqrt{3}\))(x+2-\(\sqrt{3}\))

3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 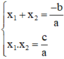
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 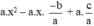
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 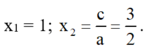
Vậy: 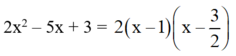

a) Phương trình 2x2 – 5x + 3 = 0 có a + b + c = 2 – 5 + 3 = 0 nên có hai nghiệm là x1 = 1, x2 = \(\dfrac{3}{2}\) nên:
2x2 – 5x + 3 = 2(x – 1)(x2 - \(\dfrac{3}{2}\)) = (x – 1)(2x – 3)
b) Phương trình 3x2 + 8x + 2 có a = 3, b = 8, b’ = 4, c = 2.
Nên ∆’ = 42 – 3 . 2 = 10, có hai nghiệm là:
x1 = \(\dfrac{-4-\sqrt{10}}{3}\), x2 = \(\dfrac{-4+\sqrt{10}}{3}\)
nên: 3x2 + 8x + 2 = 3(x - \(\dfrac{-4-\sqrt{10}}{3}\))(x - \(\dfrac{-4+\sqrt{10}}{3}\))
= 3(x + \(\dfrac{4+\sqrt{10}}{3}\))(x + \(\dfrac{4-\sqrt{10}}{3}\))