Cho hàm số y = f(x) có đạo hàm tại x = x 0 là f ' ( x 0 ) . Mệnh đề nào sau đây sai
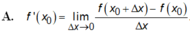
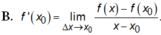
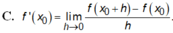
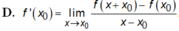
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Phương pháp:
Nếu f ' ( x ) ≥ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) đồng biến trên khoảng (a;b).
Nếu f ' ( x ) ≤ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) nghịch biến trên khoảng (a;b) Cách giải:
Quan sát đồ thị hàm số y=f’(x) , ta thấy f’(x) >0 =>Hàm số f (x) đồng biến trên
khoảng (-1;1).
=>Mệnh đề ở câu A là sai.

Đáp án là C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I

Đáp án A.
Ta có g ' x = x 2 - 2 ' f ' x 2 - 2 = 2 x . f ' x 2 - 2 ; ∀ x ∈ ℝ .
Khi đó g ' x < 0 ⇔ x . f ' x 2 - 2 < 0 ⇔ [ x < 0 f ' x 2 - 2 > 0 x > 0 f ' x 2 - 2 < 0 ⇔ [ x < 0 x 2 - 2 > 2 x > 0 x 2 - 2 < 2 ⇔ [ 0 < x < 2 x < - 2 .
Vậy hàm số nghịch biến trên khoảng - ∞ ; - 2 và (0;2) khẳng định A là sai.
Đáp án D