Cho biết hàm số f x = a x + b x 2 + 1 đạt giá trị lớn nhất bằng 4 và giá trị nhỏ nhất bằng -1. Tính giá trị của a 2 + b 3 - 44 n 2 + n + 2017 ; ∀ n ∈ N
A. 1
B. 0
C. -1
D. 2018
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Tập xác định của hàm số là ℝ .
Ta có: ![]()
Vì trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.
![]()
![]()
![]()
Khi đó f'(x) = 0 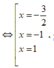 ( đều là các nghiệm đơn)
( đều là các nghiệm đơn)
Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:
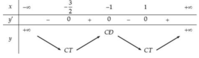
=> x = - 3 2 là điểm cực tiểu duy nhất thuộc - 2 ; - 5 4
Vậy hàm số đạt giá trị nhỏ nhất tại x = - 3 2 trên đoạn - 2 ; - 5 4
Tập xác định: D = R
Ta có
m a x x ∈ R f x = 4 ⇔ f x ≤ 4 ; ∀ x ∈ R ∃ x 0 ∈ R : f x 0 = 4 ⇔ a x + b x 2 + 1 ≤ 4 a x 0 + b x 2 0 + 1 = 4 ⇔ 4 x 2 - a x + 4 - b ≥ 0 4 x 0 2 - a x 0 + 4 - b = 0 ⇔ ∆ = a 2 + 16 b - 64 ≤ 0 ∆ = a 2 + 16 b - 64 ≥ 0 ⇔ a 2 + 16 b - 64 = 0 1
Đối với m i n x ∈ R f x = - 1 làm tương tự, ta đi đến a 2 - 4 b - 4 = 0 (2)
Giải hệ gồm (1) và (2) ta được a = ± 4 ; b = 3 .
Do n 2 + n + 2017 = n n + + 2017 là số lẻ ∀ n ∈ N nên a 2 + b 3 - 44 n 2 + n + 2017 = -1
Đáp án C