Cho đa giác (H) có n đỉnh ( n ∈ ℕ , n > 4 ) . Biết số các tam giác có 3 đỉnh là đỉnh của (H) và không có cạnh nào là cạnh của (H) gấp 5 lần số các tam giác có 3 đỉnh là đỉnh của (H) và có đúng 1 cạnh là cạnh của (H). Khẳng định nào sau đây đúng?
A. n ∈ 4 ; 12
B. n ∈ 13 ; 21
C. n ∈ 22 ; 30
D. n ∈ 31 ; 38



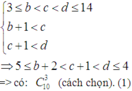
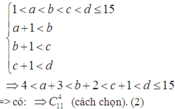


Chọn D
Lời giải. Số tam giác tạo thành có 3 đỉnh là 3 đỉnh của đa giác là C n 3
Số tam giác tạo thành có đúng 2 cạnh là cạnh của đa giác là n
Số tam giác tạo thành có đúng 1 cạnh là cạnh của đa giác là n(n-4)
(điều kiện n ∈ ℕ v à n < 4 )
→ số tam giác tạo thành không có cạnh nào là cạnh của đa giác là
Theo giả thiết, ta có
⇔ n = 35 ( t h ỏ a m ã n ) n = 4 ( l o ạ i )