Trong không gian Oxyz, cho hai điểm A(2;2;2), B(2;4;−6) và mặt phẳng (P): x+y+z=0. Tập hợp các điểm M thuộc (P) sao cho ∠ A M B = 90 ° là một đường tròn có bán kính bằng
A. 2 2
B. 17
C. 13
D. 14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Do điểm M thuộc trục Ox nên M(a;0;0)
Vì M cách đều hai điểm A, B nên MA = MB hay
![]()
Ta có:
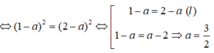
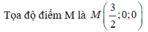

Chọn B
Gọi M (x; y; z)
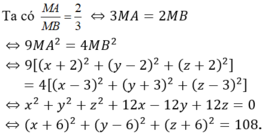
Như vậy, điểm M thuộc mặt cầu (S) tâm I(-6;6;-6) và bán kính R = √108 = 6√3. Do đó OM lớn nhất bằng
![]()

Chọn C.
Do điểm M thuộc trục Ox nên M(a,0,0)
Vì M cách đều hai điểm A, B nên MA = MB hay
![]()
![]()
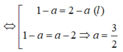
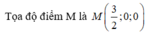

Chọn C.
Do điểm M thuộc trục Ox nên M(a,0,0)
Vì M cách đều hai điểm A, B nên MA = MB hay
![]()
![]()
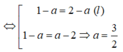
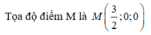
Ta có M ∈ ( P ) và ∠ A M B = 90 ° nên M thuộc mặt cầu đường kính AB là:
( S ) : x - 2 2 + y - 3 2 + z + 2 2 = 17 có tâm I(2;3-2), R = 17 .
Do đó M ∈ C = S ∩ P .
Vì vậy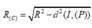
Chọn đáp án D.