Một hộp đựng 20 viên bi khác nhau được đánh số từ 1 đến 20. Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại. Hỏi có bao nhiêu cách lấy để kết quả thu được là một số chia hết cho 3?
A. 90
B. 1200
C. 384
D. 1025
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng các viên bi lẻ khi số số viên bi lẻ là lẻ
Do đó ta có các trường hợp: trong 6 viên có (1 lẻ 5 chẵn), (3 lẻ 3 chẵn), (5 lẻ 1 chẵn)
Được chọn từ 6 viên lẻ (1;3;5;7;9;11) và 5 viên chẵn (2;4;6;8;10)
Không gian mẫu: \(n\left(\Omega\right)=C_{11}^6\)
Số cách chọn thỏa mãn: \(n\left(A\right)=C_6^1.C_5^5+C_6^3.C_5^3+C_6^5.C_5^1\)
Xác suất: \(P=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)

Không gian mẫu là số sách lấy tùy ý 2 viên từ hộp chứa 12 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 2 viên bi được lấy vừa khác màu vừa khác số .
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi đỏ là 4.4=16 cách (do số bi đỏ ít hơn nên ta lấy trước, có 4 cách lấy bi đỏ. Tiếp tục lấy bi xanh nhưng không lấy viên trùng với số của bi đỏ nên có 4 cách lấy bi xanh).
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi vàng là 3.4=12cách.
● Số cách lấy 2 viên bi gồm: 1 bi đỏ và 1 bi vàng là 3.3=9 cách.
Suy ra số phần tử của biến cố A là 16+12+9=37.
Vậy xác suất cần tính 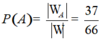 .
.
Chọn B.

Theo mình nghĩ là chọn 4 viên bi cùng màu mà nhỉ
Tổng các cách chọn 4 bi đỏ, 4 bi xanh, 4 bi trắng, 4 bi vàng:
\(C_{10}^4+C_{25}^4+C_6^4+C_9^4=10977\) (cách)

Có \(C_{24}^3\) cách chọn 3 viên bất kì.
Có \(C_8^3+C_6^3+C_{10}^3\) cách họn 3 viên bi cùng màu.
Có 6 cách chọn 3 viên bi cùng số.
\(\Rightarrow\) Có \(C_{24}^3-\left(C_8^3+C_6^3+C_{10}^3\right)-6=1822\) cách chọn 3 viên bi khác màu, khác số.
Chọn 1 viên xanh: có 6 cách
Chọn 1 viên đỏ khác số viên xanh: 7 cách
Chọn 1 viên vàng khác số viên xanh và đỏ: 8 cách
Tổng cộng: \(6.7.8=336\) cách

Không gian mẫu là số cách chọn ngẫu nhiên 3 viên bi từ hộp chứa 50 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố “3 viên bi được chọn là một số chia hết cho 3 ’’.
Trong 50 viên bi được chia thành ba loại gồm: 16 viên bi có số chia hết cho 3; 17 viên bi có số chia cho 3 dư 1 và 17 viên bi còn lại có số chia cho 3 dư 2.
Để tìm số kết quả thuận lợi cho biến cố A, ta xét các trường hợp
● Trường hợp 1. 3 viên bi được chọn cùng một loại, có ![]() cách.
cách.
● Trường hợp 2. 3 viên bi được chọn có mỗi viên mỗi loại, có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]() .
.
Vậy xác suất cần tính 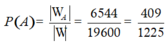
Chọn B.

Chọn A
Gọi x là số lần viên bi đỏ được chọn.
Gọi y là số lần viên bi xanh được chọn.
TH1. 1 ≤ x ≤ 6.
Có 6 cách chọn viên đỏ.
Có 5 cách chọn viên xanh.
=> Có 5.6 = 30 cách.
TH2. x = 7.
Có 6 cách chọn viên xanh.
=> Có 6 cách.
Vậy có 36 cách chọn.

Phương pháp:
Sử dụng quy tắc cộng và quy tắc nhân để làm bài toán.
Cách giải:
Vì số viên bi xanh ít hơn số viên bi đỏ nên ta lấy số viên bi xanh trước, số cách lấy 1 viên bi xanh có 6 cách .
Số cách lấy 1 viên bi đỏ và số của viên bi đỏ phải khác số của viên bi xanh đã lấy có 6 cách.
Như vậy có: 6 x 6 = 36 cách.
Chọn: A

Đáp án: D
b/ Việc lựa chọn tiến hành theo ba bước sau:
Bước 1: Chọn 1 viên bi xanh bất kì: có 6 cách thực hiện.
Bước 2: Chọn 1 viên bi đỏ bất kì: có 5 cách thực hiện.
Bước 3: Chọn 1 viên bi vàng bất kì: có 4 cách thực hiện.
Vậy theo quy tắc nhân có: 6.5.4=120 cách chọn.
Chọn C
20 viên bi khác nhau được đánh số từ 1 đến 20, chia làm ba phần:
Phần 1 gồm các viên bi mang số chia hết cho 3, có 6viên.
Phần 2 gồm các viên bi mang số chia cho 3 dư 1, có 7 viên.
Phần 3 gồm các viên bi mang số chia cho 3 dư 2, có 7 viên.
Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại, được một số chia hết cho 3 có các trường hợp sau:
Trường hợp 1: lấy được 3 viên bi ở phần 1, có C 6 3 cách.
Trường hợp 2: lấy được 3 viên bi ở phần 2, có C 7 3 cách.
Trường hợp 3: lấy được 3 viên bi ở phần 3, có C 7 3 cách.
Trường hợp 4: lấy được 1 viên bi ở phần 1, 1 viên bi ở phần 2 và 1 viên bi ở phần 3, có C 6 1 . C 7 1 . C 7 1 cách.
Vậy có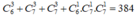 cách lấy được ba viên bi thỏa mãn yêu cầu bài toán.
cách lấy được ba viên bi thỏa mãn yêu cầu bài toán.