Xét các số thực x, y thỏa mãn x 2 + y 2 > 1 và log x 2 + y 2 ( 2 x + 3 y ) ⩾ 1 . Giá trị lớn nhất P m a x của biểu thức P = 2 x + y bằng:

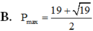
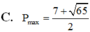
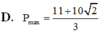
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Lời giải;
Vế 1:
Áp dụng BĐT AM-GM:
$2=(x^2+y^2)(1+1)\geq (x+y)^2\Rightarrow x+y\leq \sqrt{2}$
$x^3+\frac{x}{2}\geq \sqrt{2}x^2$
$y^3+\frac{y}{2}\geq \sqrt{2}y^2$
$\Rightarrow x^3+y^3+\frac{x+y}{2}\geq \sqrt{2}(x^2+y^2)=\sqrt{2}$
$\Rightarrow x^3+y^3\geq \sqrt{2}-\frac{x+y}{2}\geq \sqrt{2}-\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}$
-----------------------
Vế 2:
$x^2+y^2=1$
$\Rightarrow x^2=1-y^2\leq 1\Rightarrow -1\leq x\leq 1$
$y^2=1-x^2\leq 1\Rightarrow -1\leq y\leq 1$
$\Rightarrow x^3\leq x^2; y^3\leq y^2$
$\Rightarrow x^3+y^3\leq x^2+y^2$ hay $x^3+y^3\leq 1$