a) Ta có: \(\widehat{AOB}\) và \(\widehat{BOC}\) là hai góc kề bù(gt)

nên \(\widehat{AOB}+\widehat{BOC}=180^0\)

\(\Leftrightarrow\widehat{AOB}+5\cdot\widehat{AOB}=180^0\)

\(\Leftrightarrow6\cdot\widehat{AOB}=180^0\)

hay \(\widehat{AOB}=30^0\)

Ta có: \(\widehat{BOC}=5\cdot\widehat{AOB}\)(gt)

nên \(\widehat{BOC}=5\cdot30^0\)

hay \(\widehat{BOC}=150^0\)

Vậy: \(\widehat{AOB}=30^0\); \(\widehat{BOC}=150^0\)

b) Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{DOB}< \widehat{BOC}\left(75^0< 150^0\right)\)

nên tia OD nằm giữa hai tia OB và OC

\(\Leftrightarrow\widehat{COD}+\widehat{BOD}=\widehat{COB}\)

\(\Leftrightarrow\widehat{COD}=\widehat{COB}-\widehat{BOD}=150^0-75^0=75^0\)

Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{COD}< \widehat{COA}\left(75^0< 180^0\right)\) nên tia OD nằm giữa hai tia OC và OA

\(\Leftrightarrow\widehat{COD}+\widehat{AOD}=\widehat{COA}\)

\(\Leftrightarrow\widehat{AOD}=\widehat{COA}-\widehat{COD}=180^0-75^0\)

hay \(\widehat{AOD}=105^0\)

Vậy: \(\widehat{AOD}=105^0\)

a) \(\widehat{AOB}\) và \(\widehat{BOC}\) kề bù \(\Rightarrow\widehat{AOB}+\widehat{BOC}=180^0\) mà \(\widehat{BOC}=5\widehat{AOB}\)

\(\Rightarrow\widehat{AOB}+5\widehat{AOB}=180^0\Rightarrow6\widehat{AOB}=180^0\\ \Rightarrow\widehat{AOB}=30^0\Rightarrow\widehat{BOC}=150^0\).

b) Do \(OD\) nằm trong góc \(\widehat{BOC}\) \(\Rightarrow\) tia \(OD\) nằm giữa hai tia \(OB,OC\)

\(\Rightarrow\)tia \(OB\) và tia \(OA\) nằm cùng phía nhau so với tia \(OD\)

\(\Rightarrow\) tia \(OB\) nằm giữa hai tia \(OA,OD\)

\(\Rightarrow\widehat{AOD}=\widehat{AOB}+\widehat{BOD}=30^0+75^0=105^0\).

c) Nếu chỉ xét trường hợp các góc tạo bởi hai tia liên tiếp nhau:

Trên nửa mặt phẳng bờ \(AC\) có \(n+4\) tia (gồm \(4\) tia \(OA,OB,OC,OD\) và \(n\) tia vẽ thêm).

Cứ hai tia cạnh nhau tạo thành 1 góc

\(\Rightarrow\) Ta có \(n+3\) góc.

Ta có:

\(\widehat{AOB}+\widehat{BOC}=180^0\left(kebu\right)\)

\(\Rightarrow\widehat{AOB}+\frac{1}{2}\widehat{AOB}=180\)

\(\Rightarrow\frac{3}{2}\widehat{AOB}=180\)

\(\Rightarrow\widehat{AOB}=180:\frac{3}{2}=120^0\)

\(\widehat{AOB}\)= 120*

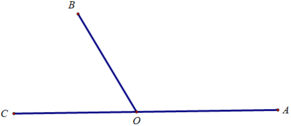
Ta có hai góc ∠BOC và ∠AOB kề bù nên ∠BOC + ∠AOB = 180o

Sai đề, Hai góc kề bù răng có 160^o

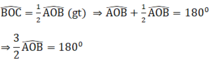
 a) vì GÓC AOB và góc BOC là hai góc kề bù nên

          AOB + BOC =180 độ

Hay    AOB + 5 X AOB = 180 độ

                     6 X AOB = 180 độ

                          AOB = 180 :6

                  Góc  AOB =30 độ

   Vì BOC = 5 x AOB

Nên BOC= 5 x 30

       BOC =150 độ

b) Vì OD phân giác của BOC nên

        BOD = DOC = BOC :2 = 150 : 2 = 75 độ

Vì OB nằm giữa hai tia OA và OB nên

         AOD = AOB + BOD

         AOD = 30 + 75

         AOD = 105 độ

a) Ta co: goc AOB+BOC=180(do) (do AOB va BOC ke bu)

\(\Rightarrow\)AOB+5AOB=180 (do BOC=5AOB)

6AOB=180

AOB=180:6=30(do)

\(\Rightarrow\)BOC=180-AOB=180-30=150(do)

b) Vì OD là tia phân giác của góc BOC => BOD=BOC : 2=150:2=75(do)

ma goc AOD=AOB+BOD=30+75=105(do)