Trong không gian Oxyz cho đường thẳng Δ có phương trình x − 2 1 = y + 3 2 = z − 1 3 . Tìm phương trình tham số của đường thẳng d là hình chiếu vuông góc của Δ trên mặt phẳng O y z .
A. x = 0 y = 3 + 2 t z = − 1 + 3 t
B. x = 0 y = − 3 + 2 t z = 1 + 3 t
C. x = − 2 + t y = 0 z = 0
D. x = 2 + t y = 0 z = 0

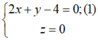
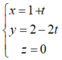

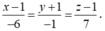


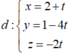
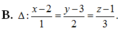





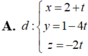
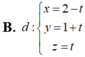
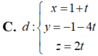
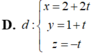


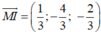 , từ đó suy ra d có một vectơ chỉ phương là
, từ đó suy ra d có một vectơ chỉ phương là 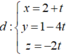

Đáp án B.
Δ : x − 2 1 = y + 3 2 = z − 1 3
Lấy M 2 ; − 3 ; 1 và N 3 ; − 1 ; 4 là hai điểm thuộc Δ.
⇒ M ' 0 ; − 3 ; 1 và N ' 0 ; − 1 ; 4 lần lượt là hình chiếu của hai điểm M; N trên mặt phẳng (Oxy)
⇒ u d → = M ' N ' → = 0 ; 2 ; 3 ⇒ d : x = 0 y = − 3 + 2 t z = 1 + 3 t