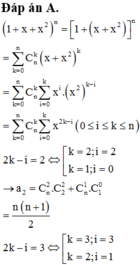
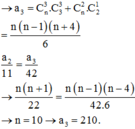
\(\left(1+x\right)^n=\sum\limits^n_{k=0}C_n^kx^k\)

Hệ số của 2 số hạng liên tiếp là \(C_n^k\) và \(C_n^{k+1}\)

\(\Rightarrow7C_n^k=5C_n^{k+1}\Leftrightarrow\frac{7n!}{k!.\left(n-k\right)!}=\frac{5n!}{\left(k+1\right)!\left(n-k-1\right)!}\)

\(\Leftrightarrow\frac{7}{n-k}=\frac{5}{k+1}\Leftrightarrow7k+7=5n-5k\)

\(\Leftrightarrow5n=12k+7\Rightarrow n=\frac{12k+7}{5}\)

\(\Rightarrow n_{min}=11\) khi \(k=4\)

2/ \(\left(x-2\right)^{100}=\sum\limits^{100}_{k=0}C_{100}^kx^k.\left(-2\right)^{100-k}\)

\(a_{97}\) là hệ số của \(x^{97}\Rightarrow k=97\)

Hệ số là \(C_{100}^{97}.\left(-2\right)^3\)

Gặp dạng hệ số đằng trước giống chỉ số của số hạng thế này thì cứ đạo hàm

\(\left(1+x+x^2\right)^{20}=a_0+a_1x+a_2x^2+...+a_{40}x^{40}\)

Đạo hàm 2 vế:

\(\Rightarrow20\left(1+x+x^2\right)^{19}\left(1+2x\right)=a_1+2a_2x+3a_3x^2+...+40a_{40}x^{39}\)

Cho \(x=1\) ta được:

\(20.3^{19}.3=a_1+2a_2+3a_3+...+40a_{40}\)

\(\Rightarrow T=20.3^{20}\)

Thanks you

Xét khai triển:

\(\left(x+1\right)^n=C_n^0+C_n^1x+C_n^2x^n+C_n^3x^3+...+C_n^nx^n\)

Đạo hàm 2 vế:

\(n\left(x+1\right)^{n-1}=C_n^1+2C_n^2x+3C_n^3x^2+...+nC_n^nx^{n-1}\)

Thay \(x=1\) vào ta được:

\(n.2^{n-1}=C_n^1+2C_n^2+3C_n^3+...+nC_n^2=256n\)

\(\Rightarrow2^{n-1}=256=2^8\Rightarrow n=9\)

Câu 2:

\(\left(x-2\right)^{80}=a_0+a_1x+a_2x^2+a_3x^3+...+a_{80}x^{80}\)

Đạo hàm 2 vế:

\(80\left(x-2\right)^{79}=a_1+2a_2x+3a_3x^2+...+80a_{80}x^{79}\)

Thay \(x=1\) ta được:

\(80\left(1-2\right)^{79}=a_1+2a_2+3a_3+...+80a_{80}\)

\(\Rightarrow S=80.\left(-1\right)^{79}=-80\)

cảm ơn anh

\(\left(1+x\right)\left(1+2x\right)...\left(1+nx\right)-1\)

\(=x+\sum\limits^n_{k=2}kx\left(1+x\right)...\left(1+\left(k-1\right)x\right)\)

\(=x+\sum\limits^n_{k=2}kx\left[\left(1+x\right)...\left(1+\left(k-1\right)x\right)-1+1\right]\)

\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left[\left(1+x\right)\left(1+2x\right)...\left(1+\left(k-1\right)x\right)-1\right]\)

\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left(\sum\limits^{k-1}_{i=1}ix\left(1+x\right)\left(1+2x\right)...\left(1-\left(i-1\right)x\right)\right)\)

Do đó tổng của các hệ số chứa \(x^2\) là: \(\sum\limits^n_{k=2}k\left(\sum\limits^{k-1}_{i=1}i\right)\)

Hay \(a_2=\sum\limits^n_{k=2}k\left(\frac{k\left(k-1\right)}{2}\right)=\sum\limits^n_{k=2}\frac{k^2\left(k-1\right)}{2}\)

Do đó:

\(S=1+\sum\limits^{2019}_{k=2}\frac{k^2\left(k-1\right)}{2}+\sum\limits^{2019}_{k=2}k^2=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k-1\right)}{2}+k^2\right)\)

\(=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k+1\right)}{2}\right)\)

thanks,đã giúp r mong bạn giúp luôn câu hình học mk vs

Ta có:

f ( 1 ) = \(a_0+a_1+....+a_{2017}\)

mà f ( x) = \(\left(x+2\right)^{2017}\)

=> \(S=f\left(1\right)=3^{2017}\)

Hiếu , tớ hỏi này tại sao lại là f(-1) hả ?

\(\left(2x+3\right)^{10}=a_0+a_1x+a_2x^2+...+a_{10}x^{10}\)

Thay \(x=1\) vào ta được:

\(5^{10}=a_0+a_1+a_2+...+a_{10}\)

Thay \(x=-1\) vào ta được:

\(\left(-2+3\right)^{10}=a_0-a_1+...+a_{10}=1^{10}=1\)

\(A=\left(x-a\right)^2.\left(x+a\right)^2\) =\(\left[\left(x-a\right)\left(x+a\right)\right]^2\) 

= \(\left(x^2-a^2\right)^2\) = \(x^4-2x^2a^2+a^4\) 

\(B=\left(1+a\right)\left(1-a\right)\left(1+a^2\right)\left(1+a^4\right)\) = \(\left(1-a^2\right)\left(1+a^2\right)\left(1+a^4\right)\) 

= \(\left(1-a^4\right)\left(1+a^4\right)\) = \(1-a^8\)