Cho ABC có AB =6 cm, AC =4,5 cm BC = 7,5 cm
a. Chứng minh tam giác ABC vuông tại A
b.Tính các góc B,C và đường cao AH của tam giác
c.tính diện tích của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 10 2021
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)
11 tháng 12 2023
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{3}{5}\)
nên \(\widehat{B}\simeq36^052'\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-36^052'=53^08'\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot7,5=4,5\cdot6=27\)
=>AH=27/7,5=3,6(cm)
13 tháng 12 2020
Giải
a. Xét \(\Delta ABC\) ta có :
\(AB^2+AC^2=\) \(6^2+4,5^2=56,25\) (cm)
\(BC^2=7,5^2=56,25\) (cm)
\(\Rightarrow\) \(\Delta ABC\) là tam giác vuông
b. - Áp dụng hệ thức về một số cạnh và đường cao trong tam giác vuông ta có :
AB.AC = BC.AH
\(\Leftrightarrow6.4,5=7,5.AH\)
\(\Leftrightarrow AH=\dfrac{6.4,5}{7,5}\)
\(\Leftrightarrow AH=3.6\) (cm)
- Trong \(\Delta ABH\perp H\) ta có :
sin B = \(\dfrac{AH}{AB}=\dfrac{3,6}{6}=0,6\)
\(\Rightarrow\) Góc B \(\approx\) \(37\) độ
\(\Rightarrow\) Góc C = 53 độ
Vậy AH = 3,6cm, góc B = 37 độ, góc C = 53 độ
24 tháng 4 2017
b)Để SMBC = SABC thì M phải cách BC một khoảng bằng AH. Do đó M phải nằm bên trên hai đường thẳng song song với BC, cách BC một khoảng bằng 3,6cm.
16 tháng 5 2022
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có \(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{B}=53^0\)
=>\(\widehat{C}=37^0\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=4,8(cm)
20 tháng 5 2019
a. Ta có: AB2 = 62 = 36
AC2 = 4,52 = 20,25
BC2 = 7,52 = 56,25
Vì AB2 + AC2 = 36 + 20,25 = 56,25 = BC2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
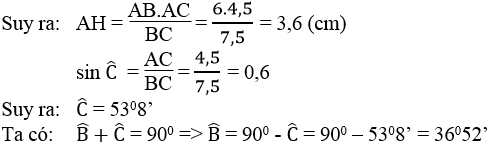b. Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời SABC = SMBC nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
11 tháng 1 2021
Độ dài chiều cao AH là:
(4,5+6):2 = 5,25 (cm)
Đáp số: 5,25 cm
nhớ k cho mình nha. Yêu nhiều!
\(a,BC^2=AB^2+AC^2\Rightarrow\Delta ABC\) vuông tại A
\(b,\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx53^0\\ AH=\dfrac{AB\cdot AC}{BC}=3,6\left(cm\right)\\ c,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot6\cdot4,5=13,5\)
a. \(\left\{{}\begin{matrix}sinC=\dfrac{AB}{BC}=53^0\\sinB=\dfrac{AC}{BC}\approx37^0\end{matrix}\right.\)
\(\Rightarrow A=180^0-\left(C+B\right)=180^0-\left(53^0+37^0\right)=90^0\left(tong3goctrong1tg\right)\)
Vậy tg ABC vuông tại A