Hai vật có khối lượng m 1 = 2 k g v à m 2 = 5 k g chuyển động với vận tốc v 1 = 5 m / s v à v 2 = 2 m / s .Tổng động lượng của hệ trong các trường hợp v 1 → v à v 2 → cùng phương, ngược chiều:
A. 0 kg.m/s
B. 3kg.m/s
C. 6kg.m/s
D. 10kg.m/s
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/Vận tốc của hai bi sau va chạm là :
Áp dụng định luật bảo toàn động lượng đối với hệ vật trước và sau khi va chạm ta có:
\(m_1v_1=\left(m_1+m_2v\right)\Rightarrow v=\frac{m_1v_2}{m_1+m_2}=\frac{500.4}{500+300}=2,5m\text{/}s\)

22/Động lượng của hệ có độ lớn là :
\(\Delta p=\sqrt{p_1^2+p_2^2}=\sqrt{\left(3.4\right)^2+\left(2.8\right)^2}\)
\(=20kgm\text{/}s\)
Vậy ta chọn C
39/Theo bảo toàn động lượng ta có:
\(m_1v_1-m_2v_2=-m_1+0\)
\(50.2-80.v_2=-50.2\Rightarrow v_2=2,5m\text{/}s\)
Vậy ta chọn B

1.
m2=2m1
chọn chiều dương cùng chiều chuyển động của bi 1
bảo toàn động lượng
\(m_1.\overrightarrow{v_1}+m_2.0=\left(m_1+m_2\right).\overrightarrow{V}\)
sau va chạm hệ chuyển động cùng chiều bi 1
chiếu lên chiều dương đã chọn
\(m_1.v_1=\left(m_1+m_2\right).V\)
\(\Leftrightarrow m_1.v_1=3m_1.V\)
\(\Rightarrow V=\)1m/s
2.
giả sử sau va chạm hệ chuyển động cùng chiều bi 1
chọn chiều dương cùng chiều chuyển động ban đầu của bi 1
bảo toàn động lượng
\(m_1.\overrightarrow{v_1}+m_2.\overrightarrow{v_2}=\left(m_1+m_2\right).\overrightarrow{V}\)
chiếu lên chiều dương đã chọn
\(\Leftrightarrow m_1.v_1-m_2.v_2=\left(m_1+m_2\right).V\)
\(\Rightarrow m_1=\)1,4kg
3.
v=36km/h=10m/s
t=2phút=120s
quãng đường đi được trong 120s
s=v.t=1200m
công lực kéo thực hiện trong 2 phút
AF=F.s.cos\(\alpha\)=24kJ
4.
72km/h=20m/s
1tấn =1000kg
theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương nằm ngang chiều dương cùng chiều chuyển động
\(F-\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương thẳng đứng chiều dương hướng lên trên
\(N=P=m.g\) (3)
gia tốc của xe là
\(v^2-v_0^2=2as\)
\(\Rightarrow a=\)2m/s2 (4)
từ (2),(3),(4)\(\Rightarrow F=\)2500N
công lực kéo là
\(A_F=F.s.cos0^0=250kJ\)
5.
để thang máy đi lên đều thì
\(F_k=P=m.g\)=8000N
công lực kéo
\(A_{F_k}=F_k.s.cos0^0\)=80kJ
6.
t=1 phút 40s=100s
để gầu nước đi lên đều thì
\(F_k=P=m.g=100N\)
cộng suất của lực kéo
\(\rho=\dfrac{A_{F_k}}{t}=\)5W

2. Áp dụng định luật bảo toàn động lượng
\(m_1v_1+m_2v_2=\left(m_1+m_2\right)v\)
\(\Rightarrow5m_1+1=\left(m_1+1\right)2,5\)
\(\Rightarrow m_1=0,6\) kg
3. Quãng đường vật đi được là
\(s=v.t=7,2.\frac{1}{6}=1,2\) km = \(1200\) m
Công của lực kéo là
\(A=F.s.\cos\alpha=40.1200.\cos60^o=24000\) J

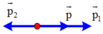
+ Vì V 2 → cùng hướng với v → 1 ⇒ p → 1 , p → 2 cùng phương, ngược chiều
⇒ p = p 1 − p 2 = 8 − 6 = 2 k g . m / s
Chọn đáp án D

![]()
Ta có: p → = p → 1 + p → 2
+ p 1 = m 1 v 1 = 2.4 = 8 k g . m / s p 2 = m 2 v 2 = 3.2 = 6 k g . m / s
+ Vì v → 2 cùng hướng với v → 1 ⇒ p → 1 , p → 2 cùng phương, cùng chiều
⇒ p = p 1 + p 2 = 8 + 6 = 14 k g . m / s
Chọn đáp án A

Động lượng vật thứ nhất:
\(p_1=m_1\cdot v_1=2\cdot4=8kg.m\)/s
Động lượng vật thứ hai:
\(p_2=m_2\cdot v_2=3\cdot2=6kg.m\)/s
a)\(v_1\uparrow\uparrow v_2\Rightarrow p=p_1+p_2=8+6=14kg.m\)/s
b)\(v_1\uparrow\downarrow v_2\Rightarrow p=p_1-p_2=8-6=2kg.m\)/s
c)\(\left(v_1;v_2\right)=90^o\Rightarrow p=\sqrt{p_1^2+p_2^2}=\sqrt{8^2+6^2}=10kg.m\)/s
d)\(\left(v_1,v_2\right)=60^o\)
\(\Rightarrow p=\sqrt{p_1^2+p_2^2+2p_1\cdot p_2\cdot cos60^o}=2\sqrt{37}kg.m\)/s

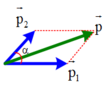
+ Vì v → 2 hướng chếch lên trên hợp với v → 2 góc 60 ° nên p → 1 ; p → 2 tạo với nhau một góc 60 °
⇒ p 2 = p 1 2 + p 2 2 + 2 p 1 p 2 cos α
⇒ p = 8 2 + 6 2 + 2.8.6 cos 60 0 = 2 37 k g . m / s
Chọn đáp án B

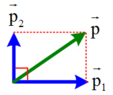
+ Vì v → 2 chếch lên trên, hợp với v → 1 góc 90 ° vuông góc
⇒ p = p 1 2 + p 2 2 = 8 2 + 6 2 = 10 k g . m / s
Chọn đáp án C
Đáp án A.
Chọn chiều dương Ox cùng chiều với v 1 →
p = m 1 v 1 x + m 2 v 2 x = 2.5 + 5 − 2 = 0 k g . m / s