Chọn đáp án B

+ Vận tốc xe đạp cũng là tốc độ dài của một điểm trên lốp xe: v=36km/h=10m/s

+ Tốc độ góc:

+ Gia tốc hướng tâm:

ω=\(\dfrac{v}{r}\)=\(\dfrac{10}{0.325}\)=30.77(rad/s)

a\(_{ht}\)=\(\dfrac{v^2}{R}\)=\(\dfrac{10^2}{0.325}\)=307,3m/s\(^2\)

Khi bánh xe đạp lăn 1 vòng thì xe chuyển động được quãng đường bằng đúng chu vi bánh xe: s = 2 π R = 2.3 , 14.0 , 32 ≈ 2 m.

Thời gian chuyển động (bánh xe quay 1 vòng): t = T = s v = 2 5 = 0 , 4 s.

Tốc độ góc ω = 2 π T = 2.3 , 14 0 , 4 = 15 , 7 rad/s.

Bán kính của bánh xe đạp là:

Khi xe đạp chuyển động thẳng đều, một điểm M trên vành bánh xe đối với người quan sát ngồi trên xe chỉ chuyển động tròn đều. (Đối với mặt đất, điểm M còn tham gia chuyển động tịnh tiến) khi đó tốc độ dài của M bằng tốc độ dài của xe: v = 12 km/h = 10/3 m/s.

Tốc độ góc của một điểm trên vành bánh đối với người ngồi trên xe là:

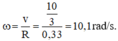
Đổi đơn vị : \(60\text{ cm}=0,6\text{ m}\) ; \(15\text{ km/h}=\frac{25}{6}\text{ m/s}\)

Vì xe đạp chuyển động với vận tốc \(\frac{25}{6}\text{ m/s}\) nên tốc độ dài của một điểm nằm trên vành bánh xe chính bằng \(\frac{25}{6}\text{ m/s}\).

Tốc độ góc của một điểm nằm trên vành bánh xe là : \(\omega=\frac{v}{r}=\frac{\frac{25}{6}}{60}=\frac{5}{72}\text{ (rad/s)}\).

Vậy tốc độ dài và tốc độ góc của 1 điểm nằm trên vành bánh xe lần lượt là : \(v=\frac{25}{6}\text{ m/s}\), \(\omega=\frac{5}{72}\text{ rad/s}\).

Tốc độ góc của 1 điểm trên vành ngoài bánh xe:

 (rad/s)

Chu kì quay của bánh xe:

 (s)

Gia tốc hướng tâm của điểm đó:

\(a_{ht}=\text{ω}^2R=60^2.0,3=1080\)