cách tính hàm số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b: Gọi A,B lần lượt là giao điểm của (d) trên hai trục Ox và Oy
Thay y=0 vào (d), ta được:
3x-3=0
hay x=1
Vậy: A(1;0)
Thay x=0 vào (d), ta được:
y=3x0-3=-3
Vậy: B(0;-3)
\(AB=\sqrt{OA^2+OB^2}=\sqrt{1^2+3^2}=\sqrt{10}\)
Khoảng cách từ O đến (d) là:
\(\dfrac{OA\cdot OB}{AB}=\dfrac{3\sqrt{10}}{10}\left(đvđd\right)\)

a: Nếu a là số nguyên dương thì TXĐ là D=R
Nếu a là số không phải nguyên dương thì TXĐ là D=R\{0}
Nếu a không là số nguyên thì TXĐ: D=R
b: \(y'=\left(x^a\right)'=\left(e^{a\cdot lnx}\right)'\)
\(=\dfrac{a}{x}\cdot e^{a\cdot lnx}=\dfrac{a}{x}\cdot x^a=a\cdot x^{a-1}\)

Đáp án B
Cho x = 0 ⇒ y = 4 ta được điểm B(0;4) thuộc trục Oy.
Cho y = 0 ⇒ x = 4 ta được điểm A(4; 0) thuộc trục Ox.
Tam giác OAB vuông tại O có OA = 4 và OB = 4 nên:
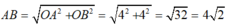

\(y'=\left(cosx\right)'\\ =\left(\dfrac{\pi}{2}-x\right)'cos\left(\dfrac{\pi}{2}-x\right)\\ =-cos\left(\dfrac{\pi}{2}-x\right)\\ =-sinx\)

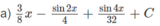
Hướng dẫn:
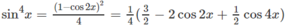
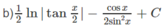
Hướng dẫn: Đặt u = cosx
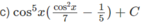
Hướng dẫn: Đặt u = cosx
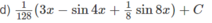
Hướng dẫn:
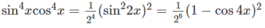

vd2 với vd3 nà