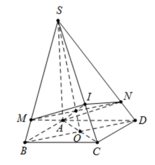
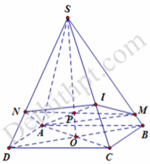
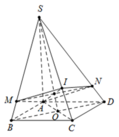
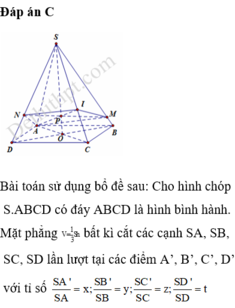
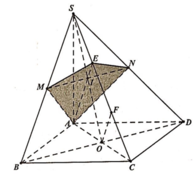
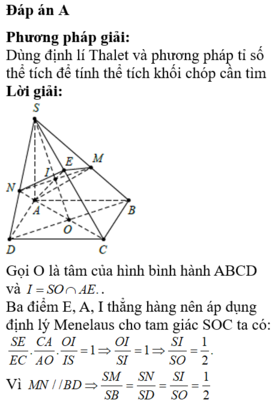
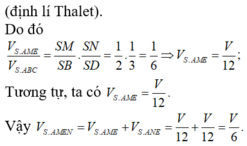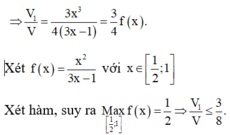Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I nằm trên cạnh SC sao cho IS=2IC. Mặt phẳng (P) chứa cạnh AI cắt cạnh SB, SD lần lượt tại M, N. Gọi V', V lần lượt là thể tích khối chóp S.AMIN và S.ABCD. Tính giá trị nhỏ nhất của tỷ số thể tích V V '
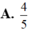
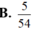
![]()
![]()