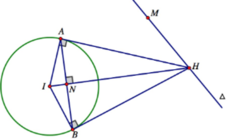
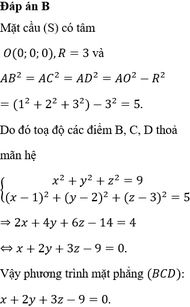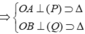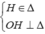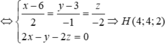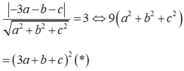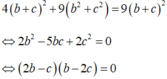Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 = 9 và điểm A(1;2;3). Từ A kẻ được ba tiếp tuyến AB,AC,AD đến mặt cầu (S) với A,B,C là các tiếp điểm. Hỏi mặt phẳng (BCD) đi qua điểm nào dưới đây ?
A. M(1;1;1).
B. N(1;1;2).
C. P(0;1;1).
D. Q(2;0;1).