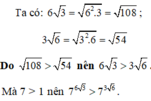
a, 6 + 6² + 6³ + 6⁴

= (6+6²) + (6³+6⁴)

^{= 6(1+6) + 63(1+6)}

= 6.7 + 6³.7

= 7(6+6³) chia hết cho 7 (đpcm)

7+7²+7³+7⁴+.....+7¹⁰

= (7+7²) + (7³+7⁴)+.....+(7⁹+7¹⁰)

=7(1+7) + 7³(1+7) +.......+ 7⁹(1+7)

= 7.8 + 7³.8 +....... + 7⁹.8

= 8(7 + 7³ +....... + 7⁹) chia hết cho 8 (đpcm)

ta có: 7+7^2+7^3+... + 7^8

=( 7+7^2) +( 7^3 +7^4)+...+(7^7 +7^8)

= 50 + 7^2(7+7^2)+...+ 7^6(7+ 7^2)

= 50 + 7^2 . 50+...+ 7^6 . 50

= 50.( 1+7^2 + ... + 7^6) chia hết cho 50

Vậy 7 + 7^2 + 7^3 + 7^4 + 7^5 +7^6 +7^7 +7^8 chia hết cho 50

k cho mk nha

3) (5⁷ - 5⁶ +5⁵) = 5⁵.(5²-5+1)= 5⁵.21 \(⋮\) 21

4) 7⁶+7⁵-7⁴= 7⁴.(7²+7-1)=7⁴.55=7³.7.11.4=7³.4.77 \(⋮\) 77

3) \(5^7-5^6+5^5=5^5.\left(5^2-5+1\right)=5^5.21⋮21\)

4) \(7^6+7^5-7^4=7^3.\left(7^3+7^2-7\right)=7^3.385=7^3.77.5⋮77\)

\(\frac{\text{(a+1)[a(a-1)-(a+3)(a+2)]}}{a+1}\)

ta có:

(a+1).a.(a-1) chia hết cho 6

(a+1).(a+3).a+2) chia hết cho 6.

(3 số tự nhiên liên kề thì chia hết cho 6);

suy ra : a(a-1)-(a+3)(a+2) chia hết cho 6

a)Ta có:\(a\left(a-1\right)-\left(a+2\right)\left(a+3\right)=a^2-a-a^2-5a-6=-6a-6\) chia hết cho 6

Câu b) tương tự.

\(M = 3^5 + 3^6 + 3^7\)

\(M = 3^5( 3^0 + 3^1 + 3^2 )\)

\(M = 3^5 ( 1 + 3 + 3^2 )\)

\(M=3^5.13⋮13\)

Ta có: \(6+6^2+6^3+6^4=\left(6+6^2\right)+6^2\times\left(6+6^2\right)=\left(6+6^2\right)\times\left(1+6^2\right)=42\times\left(1+6^2\right)=6\times7\times\left(1+6^2\right)\)

Mà \(6\times7\times\left(1+6^2\right)\) chia hết cho 7

=> \(6+6^2+6^3+6^4\) chia hết cho 7

\(6+6^2+\cdot\cdot\cdot+6^{10}\)

\(=6\cdot\left(1+6\right)+6^3\cdot\left(1+6\right)+\cdot\cdot\cdot+6^9\cdot\left(1+6\right)\)

\(=6\cdot7+6^3\cdot7+\cdot\cdot\cdot+6^9\cdot7\)

\(=7\cdot\left(6+6^3+\cdot\cdot\cdot+6^9\right)⋮7\)

\(\Rightarrow6+6^2+\cdot\cdot\cdot\cdot+6^{10}⋮7\)

\(5^1-5^9+5^8=5\left(1-5^8+5^7\right)⋮7\Leftrightarrow5^8-5^7-1⋮7\)

\(5\equiv-2\left(mod7\right)\Rightarrow5^3\equiv-1\left(mod7\right)\Rightarrow5^8\equiv4\left(mod7\right);5^7\equiv-2\left(mod7\right)\)

\(5^8-5^7-1\equiv5\left(mod7\right):v\)

\(M=3^5\left(1+3+3^2\right)=3^5.13⋮13\left(đccm\right)\)

\(M=3^5+3^6+3^7\)

\(=3^5\left(1+3+3^2\right)=3^5.13⋮13\)

Bài này mà bạn bảo của lớp 9 á