Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB=3a AD =2a , SA vuông góc ( ABCD) . Gọi M là trung điểm của AD. Khoảng cách giữa 2 đường thẳng CM và SA là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SMA}\) là góc giữa SM và đáy
\(\Rightarrow\widehat{SMA}=60^0\Rightarrow SA=AM.tan60^0=\sqrt{3a^2+\left(\dfrac{2a}{2}\right)^2}.\sqrt{3}=2a\sqrt{3}\)
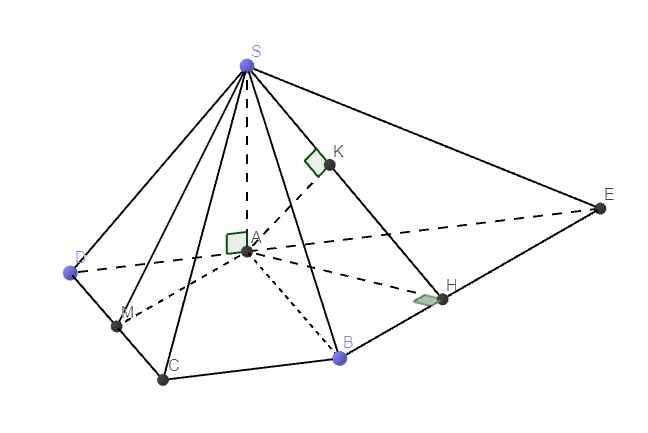
Qua B kẻ đường thẳng song song AM cắt AD kéo dài tại E
\(\Rightarrow AM||\left(SBE\right)\Rightarrow d\left(AM;SB\right)=d\left(AM;\left(SBE\right)\right)=d\left(A;\left(SBE\right)\right)\)
Từ A kẻ \(AH\perp BE\) , từ A kẻ \(AK\perp SH\Rightarrow AK=d\left(A;\left(SBE\right)\right)\)
\(\widehat{DAM}=\widehat{AEB}\) (đồng vị) , mà \(\widehat{BAH}=\widehat{AEB}\) (cùng phụ \(\widehat{ABH}\))
\(\Rightarrow\widehat{DAM}=\widehat{BAH}\)
\(\Rightarrow AH=AB.cos\widehat{BAH}=AB.cos\widehat{DAM}=\dfrac{AB.AD}{AM}=\dfrac{2a.a\sqrt{3}}{2a}=a\sqrt{3}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AH^2}+\dfrac{1}{SA^2}=\dfrac{1}{3a^2}+\dfrac{1}{12a^2}=\dfrac{5}{12a^2}\)
\(\Rightarrow AK=\dfrac{2a\sqrt{15}}{5}\)
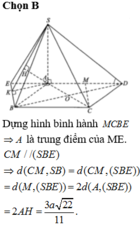

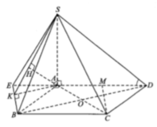
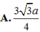
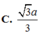
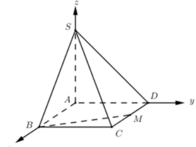

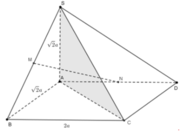
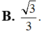
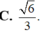
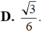

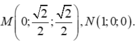
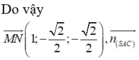
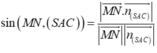
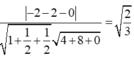
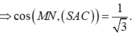
Gọi E là trung điểm AD, ta có: ME//SA (ME là đường trung bình tam giác SAD) và SA, CE chéo nhau; suy ra (MCE) vuông góc (ABCD) và không chứa SA; suy ra SA//(MCE). Suy ra, d(SA,CM) = d(SA,(MCE)) = d(A,(MCE)) = d(D,(MCE)) = d(D,EC) = ED.DC/EC = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.
Xin lỗi, mình sửa lại bài giải.
d(SA,CM) = d(A,CM) = d(D,CM) = MD.DC/CM = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.