Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng α đi qua điểm A 1 ; 2 ; - 1 sao cho khoảng cách từ B 1 ; 0 ; 0 đến mặt phẳng α lớn nhất.
A. 2 y + z - 3 = 0
B. 2 y - z = 0
C. 2 y - z - 5 = 0
D. x + 2 y - z - 6 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Gọi giao điểm của Δ và d là B nên ta có: B (3+t;3+3t;2t) ![]()
Vì đường thẳng Δ song song với mặt phẳng (α) nên:
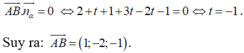
Phương trình đường thẳng Δ đi qua A và nhận 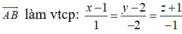

mặt phẳng
α
chứa trục Oz nên phương trình có dạng ![]()
Lại có
α
đi qua điểm P(2;-3;5) nên ![]()
Vậy phương trình mặt phẳng α : 3x + 2y = 0
Chọn C.

Đáp án B.
Vì β song song với α nên loại đáp án C và D.
Thử trực tiếp thấy điểm A 1 ; 2 ; 3 thuộc mặt phẳng x − 4 y + z + 4 = 0 .
Do đó đáp án đúng là B.
Chọn đáp án C