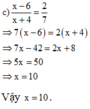
a) 9x-1/4=3/2

=>9x=3/2+1/4

=>9x=7/4

=>x=7/4:9

=>x=7/36

Vậy x=7/36

b)(4x+2):2,5=3,2:0,5

=>(4x+2):2,5=6,4

=>4x+2=6,4.2,5

=>4x+2=16

=>4x=16-2

=>4x=14

=>x=14:4

=>x=7/2

Vậy x=7/2

c) 5,4/x-2=6/7

=>5,4/x=6/7+2

=>5,4/x=20/7

=>x=5,4 :20/7

=>x=1,89

Vậy x= 1,89

d) 0,5:2=3:(2x+7)

=>3:(2x+7)=0,25

=>2x+7=3:0,25

=>2x+7=12

=>2x=12-7

=>2x=5

=>x=5/2

Vậy x=5/2

a) 9x-1/4=3/2

=>9x=3/2+1/4

=>9x=7/4

=>x=7/4:9

=>x=7/36

Vậy x=7/36

b)(4x+2):2,5=3,2:0,5

=>(4x+2):2,5=6,4

=>4x+2=6,4.2,5

=>4x+2=16

=>4x=16-2

=>4x=14

=>x=14:4

=>x=7/2

Vậy x=7/2

c) 5,4/x-2=6/7

=>5,4/x=6/7+2

=>5,4/x=20/7

=>x=5,4 :20/7

=>x=1,89

Vậy x= 1,89

d) 0,5:2=3:(2x+7)

=>3:(2x+7)=0,25

=>2x+7=3:0,25

=>2x+7=12

=>2x=12-7

=>2x=5

=>x=5/2

Vậy x=5/2

a: =>x-2=6,3

=>x=8,3

d:=>|x-3|=14

=>x-3=14 hoặc x-3=-14

=>x=17 hoặc x=-11

a, \(\frac{x-6}{x+4}=\frac{2}{7}\Rightarrow7x-42=2x+8\)ĐK : \(x\ne-4\)

\(\Leftrightarrow5x=50\Leftrightarrow x=10\)(tm)

b, \(\left(x+5\right):2\frac{1}{2}=\frac{40}{x+5}\)ĐK : \(x\ne-5\)

\(\Leftrightarrow\frac{5\left(x+5\right)}{2}=\frac{40}{x+5}\Rightarrow5\left(x+5\right)^2=80\Leftrightarrow\left(x+5\right)^2=16\)

TH1 : \(x+5=4\Leftrightarrow x=-1\)

TH2 : \(x+5=-4\Leftrightarrow x=-9\)

a) \(\left(\frac{1}{3}.x\right):\frac{2}{3}=\frac{7}{4}:\frac{2}{5}\)

\(\left(\frac{1}{3}.x\right):\frac{2}{3}=\frac{35}{8}\)

\(\Rightarrow\frac{1}{3}.x=\frac{35}{8}.\frac{2}{3}\)

\(\Rightarrow\frac{1}{3}.x=\frac{35}{12}\)

\(\Rightarrow x=\frac{35}{12}:\frac{1}{3}\)

\(\Rightarrow x=\frac{35}{4}\)

Vậy \(x=\frac{35}{4}\)

a) x= \(\frac{35}{4}\)

Bài 1:

a. 

Ta có tỉ lệ thức: 4,5 x 14,4 = 6 x 10,8

\(\Rightarrow\frac{4,5}{6}=\frac{10,8}{14,4};\frac{4,5}{10,8}=\frac{6}{14,4};\frac{6}{4,5}=\frac{14,4}{10,8};\frac{10,8}{4,5}=\frac{14,4}{6}\)

b. 

Ta có tỉ lệ thức 1: 4 x 1024 = 16 x 256

\(\Rightarrow\frac{4}{16}=\frac{256}{1024};\frac{4}{256}=\frac{16}{1024};\frac{16}{4}=\frac{1024}{256};\frac{256}{4}=\frac{1024}{16}\)

Ta có tỉ lệ thức 2: 16 x 64 = 4 x 256

\(\Rightarrow\frac{16}{4}=\frac{256}{64};\frac{16}{256}=\frac{4}{64};\frac{4}{16}=\frac{64}{256};\frac{256}{16}=\frac{64}{4}\)

Bài 2:

Áp dụng t/c DTSBN. ta có:

\(\frac{x}{11}=\frac{y}{7}=\frac{x+y}{11+7}=\frac{-54}{18}=-3\)

\(\Rightarrow x=11.\left(-3\right)=-33\)

\(\Rightarrow y=7.\left(-3\right)=-21\)

-0,52:x=-9,36

-0,52:x=-4/7

x=-0,52:-4/7

x=0.91

\(a,\dfrac{4}{x}=\dfrac{8}{x+1}\left(x\ne0;x\ne-1\right)\Rightarrow4x+4=8x\\ \Rightarrow x=1\\ b,\dfrac{x}{7}=\dfrac{x+16}{35}\Rightarrow35x=7x+112\\ \Rightarrow28x=112\Rightarrow x=4\\ c,\dfrac{6}{x-3}=\dfrac{7}{x-5}\left(x\ne3;x\ne5\right)\Rightarrow6x-30=7x-21\\ \Rightarrow x=-9\\ d,\dfrac{44-x}{3}=\dfrac{x-12}{5}\Rightarrow220-5x=3x-36\\ \Rightarrow8x=256\Rightarrow x=32\)

a) 2/7 : x = 11/6 : 7/12

2/7 : x = 22/7

x = 2/7 : 22/7

x = 1/11

b) (2 - x)/3 = -3/(x - 2)

(2 - x)(x - 2) = -3.3

-(x - 2)² = -9

(x - 2)² = 9

x - 2 = 3 hoặc x - 2 = -3

*) x - 2 = 3

x = 3 + 2

x = 5

*) x - 2 = -3

x = -3 + 2

x = -1

Vậy x = -1; x = 5

c) (x - 1)/(x + 2) = 2/3

3(x - 1) = 2(x + 2)

3x - 3 = 2x + 4

3x - 2x = 4 + 3

x = 7

a) 2/7 : x = 11/6 : 7/12

2/7 : x = 22/7

x = 2/7 : 22/7

x = 1/11

b) (2 - x)/3 = -3/(x - 2)

(2 - x)(x - 2) = -3.3

-(x - 2)² = -9

(x - 2)² = 9

x - 2 = 3 hoặc x - 2 = -3

*) x - 2 = 3

x = 3 + 2

x = 5

*) x - 2 = -3

x = -3 + 2

x = -1

Vậy x = -1; x = 5

c) (x - 1)/(x + 2) = 2/3

3(x - 1) = 2(x + 2)

3x - 3 = 2x + 4

3x - 2x = 4 + 3

x = 7

\(\begin{array}{l}a)\dfrac{x}{6} = \dfrac{{ - 3}}{4}\\x = \dfrac{{( - 3).6}}{4}\\x = \dfrac{{ - 9}}{2}\end{array}\)

Vậy \(x = \dfrac{{ - 9}}{2}\)

\(\begin{array}{l}b)\dfrac{5}{x} = \dfrac{{15}}{{ - 20}}\\x = \dfrac{{5.( - 20)}}{{15}}\\x = \dfrac{{ - 20}}{3}\end{array}\)

Vậy \(x = \dfrac{{ - 20}}{3}\)

Câu 1:

a)Áp dụng tc dãy tỉ:

\(\frac{x}{3}=\frac{y}{7}=\frac{x+y}{3+7}=\frac{20}{10}=2\)

\(\Rightarrow\begin{cases}\frac{x}{3}=2\Rightarrow x=6\\\frac{y}{7}=2\Rightarrow y=14\end{cases}\)

b)Áp dụng tc dãy tỉ:

\(\frac{x}{5}=\frac{y}{2}=\frac{x-y}{5-2}=\frac{6}{3}=2\)

\(\Rightarrow\begin{cases}\frac{x}{5}=2\Rightarrow x=10\\\frac{y}{2}=2\Rightarrow y=4\end{cases}\)

Câu 2:

a)\(\frac{x}{7}=\frac{18}{14}\Rightarrow14x=18\cdot7\)

\(\Rightarrow14x=126\)

\(\Rightarrow x=9\)

b và c đề có vấn đề

Câu 1:

a) Giải:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{x}{3}=\frac{y}{7}=\frac{x+y}{3+7}=\frac{20}{10}=2\)

+) \(\frac{x}{3}=2\Rightarrow x=6\)

+) \(\frac{y}{7}=2\Rightarrow y=14\)

Vậy cặp số \(\left(x,y\right)\) là \(\left(6,14\right)\)

b) Giải:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{x}{5}=\frac{y}{2}=\frac{x-y}{5-2}=\frac{6}{3}=2\)

+) \(\frac{x}{5}=2\Rightarrow x=10\)

+) \(\frac{y}{2}=2\Rightarrow y=4\)

Vậy cặp số \(\left(x,y\right)\) là \(\left(10,4\right)\)

Câu 3:

Giải:

Áp dụng tính chất dãy tỉ số bằng nhau:

\(\frac{x}{2}=\frac{y}{4}=\frac{z}{6}=\frac{x-y+z}{2-4+6}=\frac{8}{4}=2\)

+) \(\frac{x}{2}=2\Rightarrow x=4\)

+) \(\frac{y}{4}=2\Rightarrow y=8\)

+) \(\frac{z}{6}=2\Rightarrow z=12\)

Vậy bộ số \(\left(x,y,z\right)\) là \(\left(4,8,12\right)\)

Câu 4:

Giải: 

Đặt \(\frac{a}{b}=\frac{c}{d}=k\)

\(\Rightarrow a=bk,c=dk\)

Ta có: 

\(\frac{a+b}{a-b}=\frac{bk+b}{bk-b}=\frac{b\left(k+1\right)}{b\left(k-1\right)}=\frac{k+1}{k-1}\) (1)

\(\frac{c+d}{c-d}=\frac{dk+d}{dk-d}=\frac{d\left(k+1\right)}{d\left(k-1\right)}=\frac{k+1}{k-1}\) (2)

Từ (1) và (2) suy ra \(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)