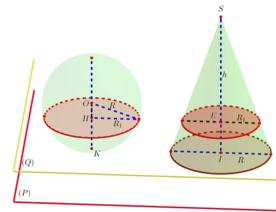
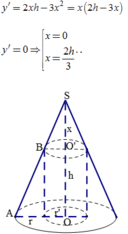
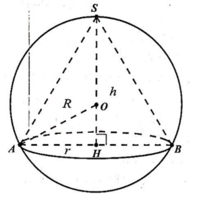
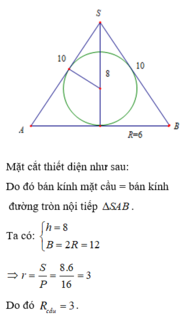
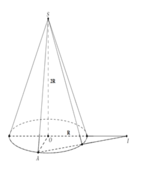
Cho hình cầu tâm O bán kính R , tiếp xúc với mặt phẳng (P) . Một hình nón tròn xoay có đáy nằm trên (P), có chiều cao h = 15 , có bán kính đáy bằng R . Hình cầu và hình nón nằm về một phía đối với mặt phẳng (P) . Người ta cắt hai hình đó bởi mặt phẳng (Q) song song với (P) và thu được hai thiết diện có tổng diện tích là S . Gọi x là khoảng cách giữa (P) và (Q), ( 0 < x ≤ 5 ) . Biết rằng S đạt giá trị lớn nhất khi x = a b (phân số a b tối giản). Tính giá trị T =a+b .
![]()
![]()
![]()
![]()


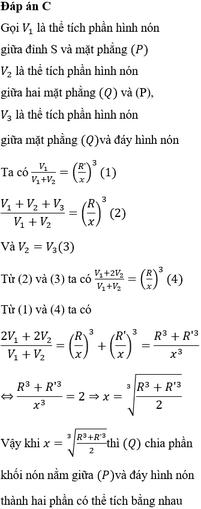
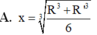
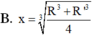
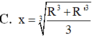
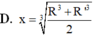

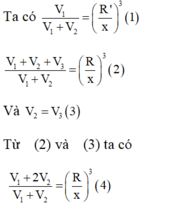


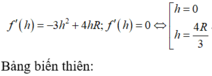
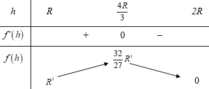
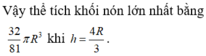

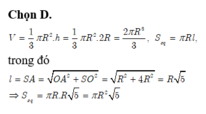


Đáp án đúng : B