Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng
60
°
. Tính tỉ số thể tích của hình trụ (N) và hình nón (T). A.
V
T
V
N
=
2
6
B.
V
T
V
N
=
2
...
Đọc tiếp
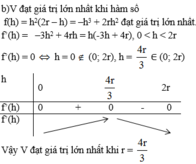
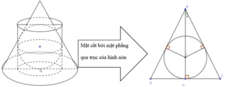
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một hình nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (N) và hình nón (T).
A. V T V N = 2 6
B. V T V N = 2 3
C. V T V N = 3 2
D. Đáp án khác
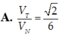
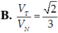
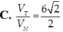
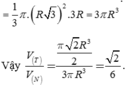
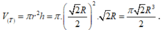
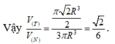
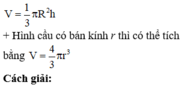
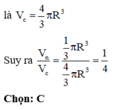
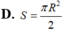
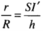
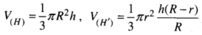
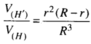
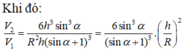
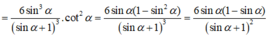
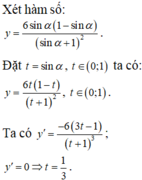
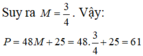
Đáp án A.
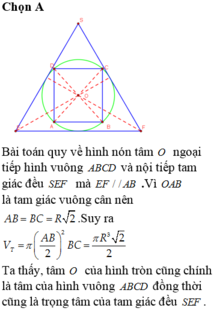
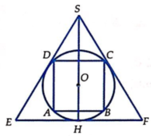
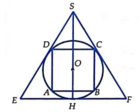
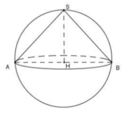
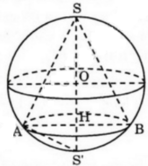
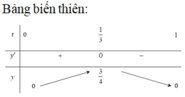
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ S E F đều” (hình vẽ).
Hình vuông ABCD nội tiếp đường tròn (O) nên
A B = B D = 2 R = A B 2 ⇔ A B = 2 R .
⇒ Bán kính đáy và chiều cao của hình trụ (T) lần lượt là r = A B 2 = 2 R 2 và h = A B = 2 R .
Thể tích khối trụ là V T = πr 2 h = π . 2 R 2 2 . 2 R = π 2 R 3 2 .
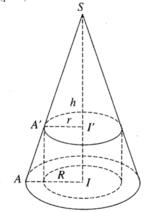
Ta có ∆ S E F đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của Δ S E F .
Gọi H là trung điểm của EF thì S H = 3 O H = 3 R ⇒ H F = S H . tan 30 ° = R 3
⇒ Bán kính đáy và chiều cao của hình nón (N) lần lượt là H F = R 3 và S H = 3 R . Thể tích khối nón là V N = 1 3 π . HF 2 . SH = 1 3 π R 3 2 . 3 R = 3 πR 3 .
Vậy V T V N = π 2 R 3 2 3 πR 3 = 2 6 .