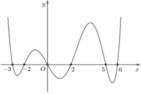
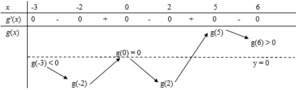
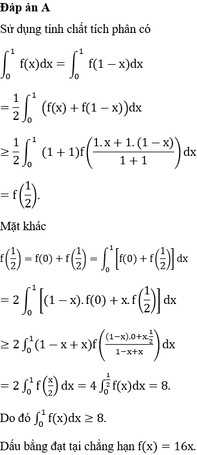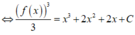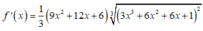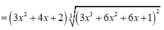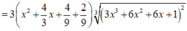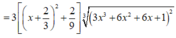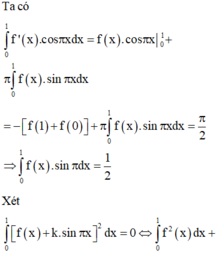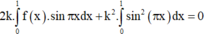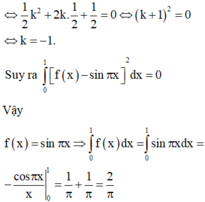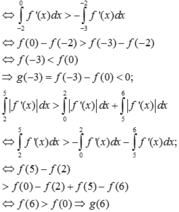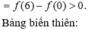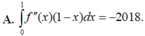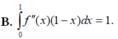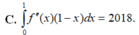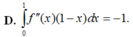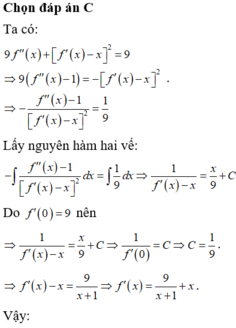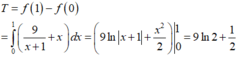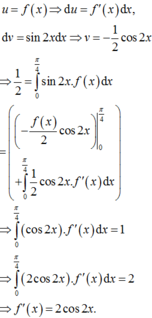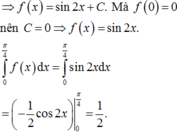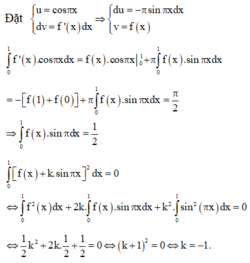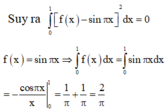Cho hàm số f(x) liên tục trên đoạn [0;1] thoả mãn với mọi x , y , α , β ∈ [ 0 ; 1 ] và α 2 + β 2 > 0 ta có α f ( x ) + β f ( y ) ≥ ( α + β ) f α x + β y α + β . Biết f(0)=0, ∫ 0 1 2 f ( x ) d x = 2 . Giá trị nhỏ nhất của tích phân ∫ 0 1 f ( x ) d x bằng
A. 8.
B. 4.
C. 2 2 .
D. 2.