Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x - 1 2 + y - 2 2 + z - 3 2 = 4 . Xét đường thẳng d : x = 1 + t y = - m t z = ( m - 1 ) t với m là tham số thực. Giả sử (P) và (P') là hai mặt phẳng chứa d, tiếp xúc với (S) lần lượt tại T và T'. Khi m thay đổi, tính giá trị nhỏ nhất của độ dài đoạn thẳng TT'.
A. 2
B. 2 11 3
C. 4 13 5
D. 2 2



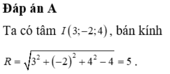
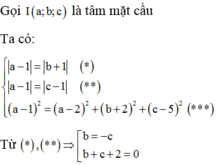
Chọn C
Mặt cầu (S) có tâm I(1;2;3), bán kính R =2. Mặt phẳng (ITT') cắt d tại điểm M (như hình vẽ trên). Gọi H là giao điểm của TT' và MI.
Do TT' = 2TH nên
Nhận xét rằng với
nên khi thay đổi ta luôn có
cố định. Vì thế
Từ đó ta có:
Ta kiểm tra điều kiện đủ của bài toán, tức là chứng minh rằng hình chiếu vuông góc của I lên (P) thuộc vào đường thẳng d.
Gọi d' là đường thẳng qua I và vuông góc với ta có:
Gọi M là hình chiếu vuông góc của I lên (P) ta có:
Xét hệ
Vậy với m = 1 5 thì độ dài của TT' nhỏ nhất.