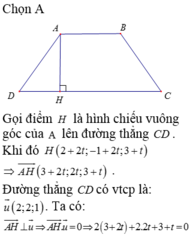
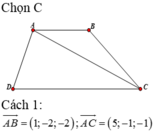
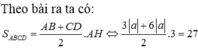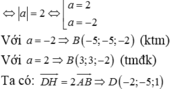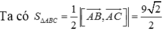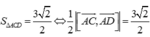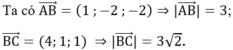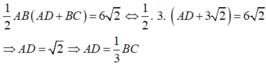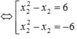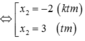Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD=2AB và diện tích bằng 28, đỉnh A ( - 1 ; - 1 ; 0 ) , phương trình đường thẳng chứa cạnh CD là x - 2 2 = y + 1 2 = z - 3 1 . Tìm tọa độ điểm D biết hoành độ điểm B lớn hơn hoành độ điểm A.
![]()
![]()
![]()
![]()