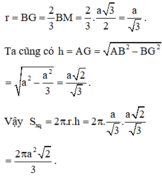Cho tứ diện ABCD đều cạnh 3a. Tính diện tích xung quanh của hình nón có đỉnh là A, đường tròn đáy là đường tròn ngoại tiếp tam giác BCD.
A. 3 3 πa 2
B. 3 2 2 πa 2
C. 3 3 2 πa 2
D. 9 4 πa 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Bán kính đáy của hình nón bằng bán kính ngoại tiếp đáy
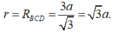
Chiều cao nón bằng chiều cao của tứ diện
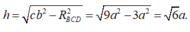
Vậy
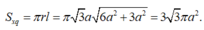

![]()
Diện tích xung quanh của hình trụ là:
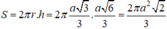
Thể tích của khối trụ là;
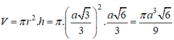

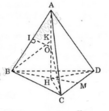
a,+) Từ A vẽ AH _|_ (BCD) (theo giả thiết AB = AC = AD)
Nên \(\Delta ABH=\Delta ACH=\Delta ADH\)
=> HB = HC = HD
Vậy H là tâm đường tròn ngoại tiếp tam giác BCD
+) Ta có: \(AH=\sqrt{AB^2-BH^2}\) với \(BH=\dfrac{2}{3}BM=\dfrac{2}{3}\cdot\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow AH=\sqrt{a^2-\dfrac{3a^2}{9}}=\dfrac{a\sqrt{6}}{3}\)
b, Ta có: \(H=AH=\dfrac{a\sqrt{6}}{3};r=BH=\dfrac{a\sqrt{3}}{3}\)
Diện tích xung quanh hình trụ là:
\(S_{xq}=2\pi rh=2\pi.\dfrac{a\sqrt{3}}{3}.\dfrac{a\sqrt{6}}{3}=\dfrac{2\pi\pi^2\sqrt{2}}{3}\)
Thể tích khối trụ là:
\(V=\pi r^2h=\pi\left(\dfrac{a\sqrt{3}}{3}\right)^2.\dfrac{a\sqrt{6}}{3}=\dfrac{\pi a^3\sqrt{6}}{9}\)

Đáp án D
Gọi r là bán kính đường tròn đáy và h là chiều cao tứ diện, ta có Sxq = 2 π .r.h.
Nếu gọi M là trung điểm CD và G là trọng tâm tam giác BCD thì ta có
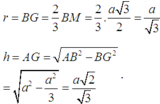
Vậy
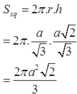

Đáp án D
Gọi r là bán kính đường tròn đáy và h là chiều cao tứ diện, ta có S x q = 2 π . r . h
Nếu gọi M là trung điểm CD và G là trọng tâm tam giác BCD thì ta có