Trong không gian Oxyz, cho các điểm
A
2
;
1
;
−
1
,
B
3
;
0
;
1
,
C
2
;
−
1
;
3
và điểm D nằm trên trục Oy sao cho thể tích khối tứ diện ABCD bằng 5. Tọa độ điểm D là A.
D
0
;
−
7
;
0
B.
D
0
;
8
;
0
C.
D
1
;
...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A 2 ; 1 ; − 1 , B 3 ; 0 ; 1 , C 2 ; − 1 ; 3 và điểm D nằm trên trục Oy sao cho thể tích khối tứ diện ABCD bằng 5. Tọa độ điểm D là
A. D 0 ; − 7 ; 0
B. D 0 ; 8 ; 0
C. D 1 ; − 7 ; 0 D 0 ; 8 ; 0
D. D 0 ; 7 ; 0 D 0 ; − 8 ; 0
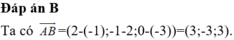
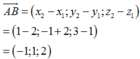
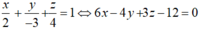
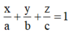
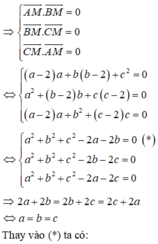
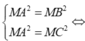
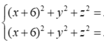
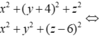
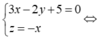
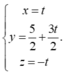
Đáp án C
Điểm D ∈ O y nên D 0 ; y ; 0 . Suy ra A D → = − 2 ; y − 1 ; 1 .
Ta có A B → = 1 ; − 1 ; 2 , A C → = 0 ; − 2 ; 4 ⇒ A B → , A C → = 0 ; − 4 ; − 2 .
Khi đó V A B C D = 1 6 A B → , A C → . A D → = 1 6 − 4 y + 2 = 2 y − 1 3 .
Từ giả thiết ta có
V A B C D = 5 ⇔ 2 y − 1 3 = 5 ⇔ y = 8 y = − 7
. Vậy D 0 ; − 7 ; 0 D 0 ; 8 ; 0 .
Tính tích có hướng A B → , A C → bằng MTCT: