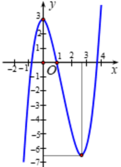
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ bên dưới. Đặt g(x)=f [f(x)]. Tìm số nghiệm của phương trình g'(x) = 0
A. 4
B. 6
C. 2
D. 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Kí hiệu trên đồ thị như hình bên.
Đặt u = f x . Ta có g x = f f x = f u .
g
'
x
=
u
'
.
f
'
u
=
f
'
x
.
f
'
u
g
'
x
=
0
⇔
f
'
x
=
0
f
'
u
=
0
f ' x = 0 ⇔ x 1 = 0 x 2 = a 2 < a < 3 (nhìn hình để xác định a).
f
'
u
=
0
⇔
u
=
x
1
u
=
x
2
⇔
f
x
=
x
1
=
0
f
x
=
x
2
=
a
2
<
a
<
3
f
x
=
0
⇔
x
∈
b
;
1
;
c
=
x
3
;
x
4
;
x
5
f x = a (nhìn vào đồ thị thể hiện bên ta thấy đồ thị hàm số f x cắt đường thẳng y = a (với 2 < a < 3 ) tại ba điểm phân biệt do vậy phương trình f x = a có ba nghiệm phân biệt x 6 ; x 7 ; x 8 .
Rõ ràng x 1 ,..., x 8 là đôi một khác nhau.
Kết hợp lại thì phương trình g ' x = 0 có 8 nghiệm phân biệt.

Đáp án C.
Ta có ![]() ∀
x
∈
R
∀
x
∈
R
Khi đó ![]()
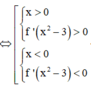
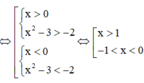
Suy ra hàm số đồng biến trên khoảng (–1;0) và (1;+ ∞)
Ta có
+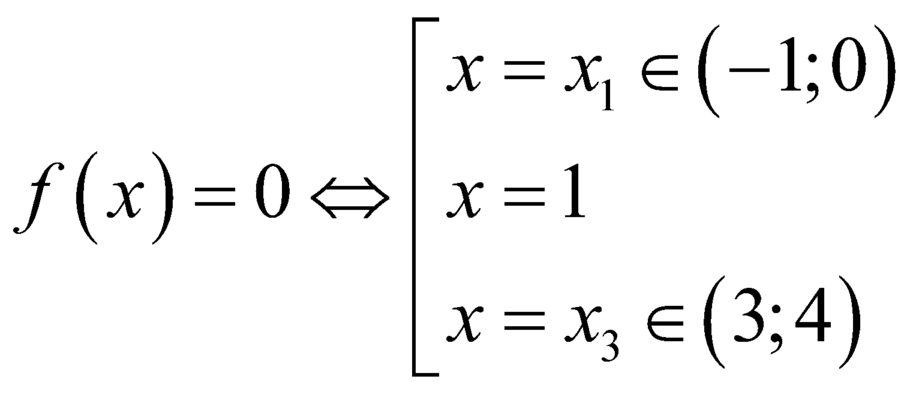
+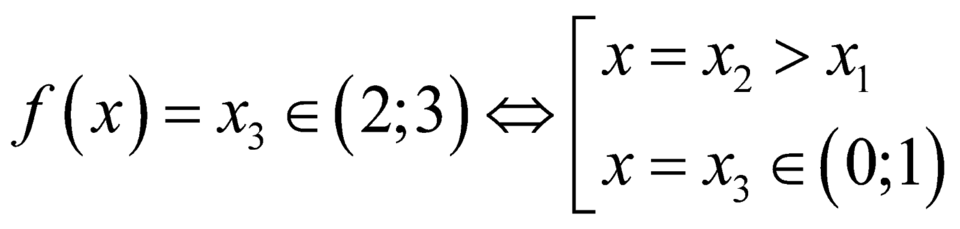 .
.
Vậy phương trình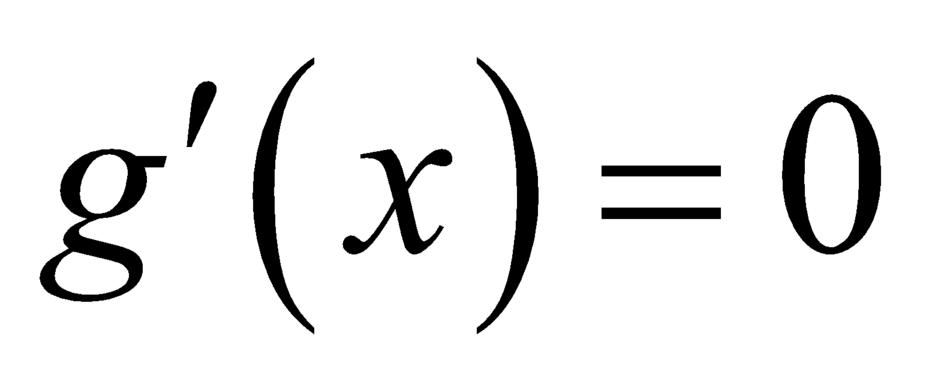 có 8 nghiệm phân biệt.
có 8 nghiệm phân biệt.
Đáp án D