Cho S : x 2 + y 2 + z 2 = 3 và d : x - 1 2 = y + 1 - 2 = z - 1 . Biết d ∩ S = E , F . Tính EF.
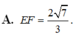
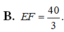
![]()
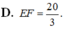
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng bđt cauchy schwarz dạng engel ta có :
\(VP=\frac{x^2}{1}+\frac{y^2}{1}+\frac{z^2}{1}\le\frac{\left(x+y+z\right)^2}{3}=3\)
Dấu = xảy ra khi và chỉ khi \(x=y=z=1\)
Vậy \(Max_S=3\)khi \(x=y=z=1\)

ta có (x+y+z)3 = (x+y)3 + [3(x+y)2z + 3(x+y).z2 ]+ z3 = (x3 + 3x2y + 3xy2 + y3 )+ 3 (x+y).z.(x+y+z) + z3
= x3 + y3 + z3 + 3xy (x+y) + 3z(x+y) (vì x+y + z = 1)
= 1 + 3(x+y).(xy + z) = 1+ 3(x+y)(xy+z) = 1
=> x+y = 0 hoặc xy +z = 0
Nếu x+ y = 0 => x=-y và z = 1 => S = x2013 + (-x)2015 + 12017 + 2019 = x2013 - x2015 +2020 (có thể đề là y2013)
Nếu xy + z = 0 => z = -xy => x + y -xy - 1 = 0 => x(1-y) -(1-y) = 0 => (x-1)(1-y) = 0 => x = 1 hoặc y = 1
x = 1 => z = -y làm tương tự như trên
* đề nên sửa số mũ của x, y, z đều bằng nhau và bằng số lẻ

Chọn đáp án A