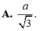
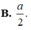
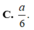
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Phương pháp: Phương pháp tọa độ.
Cách giải: Chọn hệ trục tọa độ như hình vẽ, chọn a = 1
Chọn D.
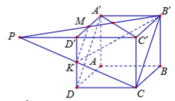
Cách 1: Trong mặt phẳng (CDD'C) gọi P là giao điểm của CK và C'D'.
Suy ra KD' là đường trung bình của ∆ PCC' => D' là trung điểm của PC'.
Trong mặt phẳng (A'B'C'D') gọi M là giao điểm của PB' và A'D'
Ta có 
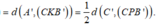
Tứ diện PCC'B' có C'P, C'B và C'B đôi một vuông góc với nhau.
Đặt 
thì 
Suy ra 
Vậy 
Cách 2: (Đã học chương 3, HH12)
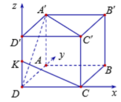
Chọn hệ trục tọa độ sao cho: D(0;0;0), trục Ox trùng với cạnh DC, trục Oy trùng với cạnh DA, trục Oz trùng với cạnh DD', chọn a = 1.
Ta có : 
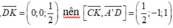
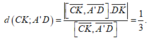
Chọn đáp án B
Gọi M là trung điểm BB' 
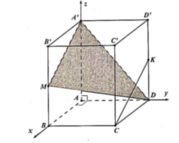
Gắn hệ trục tọa độ như hình vẽ:
Ta có: D(0;a;0), A'(0;0;a), C(a;a;0), M(a;0; a 2 )
Khi đó: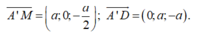 
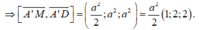
Mặt phẳng (A’MD) đi qua điểm và nhận làm vectơ pháp tuyến là:
Khi đó: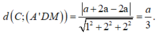 
Chọn B
Gọi M là trung điểm BB'. Ta có: CK // A'M => CK // (A'MD)
Khi đó d(CK, A'D) = d (CK, (A'MD)). Gắn hệ trục tọa độ như hình vẽ:
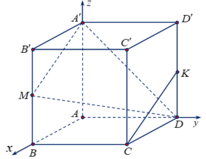
Ta có: A(0;0;0), B(a;0;0), D(0;a;0), A'(0;0;a), B'(a;0;a), C(a;a;0), M(a;0;a/2).
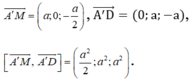
Vậy mặt phẳng (A'MD) nhận 
làm vectơ pháp tuyến.
Phương trình (A'MD) là x + 2y + 2z - 2a = 0
Do đó: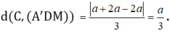 
Chọn D