Cho hàm số y= 2 x 2 - 1 . Chọn phát biểu đúng.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Điều kiện để hàm số xác định là 2 x 2 − x − 1 > 0 ⇔ x > 1 x < − 1 2 *
Với điều kiện * ta có 4 x − 1 2 x 2 − x − 1 ln 2 > 0 ⇔ x ∈ 1 ; + ∞ , y ' < 0 ⇔ x ∈ − ∞ ; − 1 2 ⇒
Hàm số nghịch biến trên − ∞ ; − 1 2 , đồng biến trên 1 ; + ∞

Đáp án C.
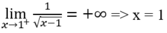 là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.
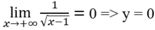 là đường tiệm cận ngang của đồ thị hàm số.
là đường tiệm cận ngang của đồ thị hàm số.

Chọn A.
(I) sai f xđ trên R
(II) sai hs có 2 điểm cực trị
(III) ,(IV) đúng

Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :
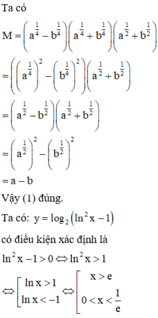
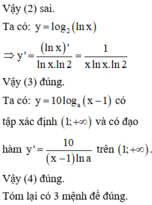

Đáp án D
Phương pháp:
Đánh giá từng đáp án.
Cách giải:
(1) Hàm số y = log2x đồng biến trên khoảng (0;+∞): đúng, do 2 > 1
(2) Hàm số y = log2x có một điểm cực tiểu: sai, hàm số y = log2x luôn đồng biến trên (0;+∞)
(3) Đồ thị hàm số y = log2x có tiệm cận: đúng, tiệm cận đó là đường x = 0
Số phát biểu đúng là 2.
Đáp án C